
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:填空题
飞机着陆后滑行的距离S(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是s=60t﹣1.2t2,那么飞机着陆后滑行_____秒停下.
查看答案和解析>>
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:填空题
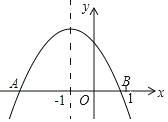
已知二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论,①abc>0; ②a+b+c<0;③b=2a;④a+b>0;则其中正确的结论是_____(只填写序号).
查看答案和解析>>
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:填空题
如图抛物线y=x2+2x﹣3与x轴交于A、B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为_____.

查看答案和解析>>
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:填空题
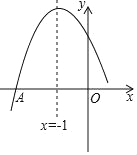
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=﹣1,与x轴的一个交点是A(﹣3,0)其图象的一部分如图所示,对于下列说法:①2a=b;②abc>0,③若点B(﹣2,y1),C(﹣ ,y2)是图象上两点,则y1<y2;④图象与x轴的另一个交点的坐标为(1,0).其中正确的是_____(把正确说法的序号都填上)
,y2)是图象上两点,则y1<y2;④图象与x轴的另一个交点的坐标为(1,0).其中正确的是_____(把正确说法的序号都填上)
查看答案和解析>>
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:解答题
已知二次函数y=﹣2x2﹣4x+6.
(1)求出函数的顶点坐标、对称轴以及描述该函数的增减性.
(2)求抛物线与x轴交点和y轴交点坐标;并画出它的大致图象.
(3)当﹣2<x<4时.求函数y的取值范围.
查看答案和解析>>
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:解答题
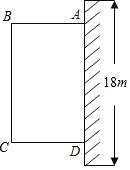
为了改善小区环境,某小区决定要在一块边靠墙(墙长18m)的空地,修建一个矩形绿地ABCD,绿地一边靠墙,另三边用总长为40m的栅栏围住(如图),设AB边为xm,绿地面积为ym2.
(1)求y与x之间的函数关系,并求出自变量x的取值范围;
(2)绿地的面积能不能为200m2?如果能,求出x的值,如果不能,请说明理由.
查看答案和解析>>
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:解答题
某种水果进价为每千克20元,市场调查发现,该水果每天的销售量y(千克)与售价x(元/千克)有如下关系:y=﹣2x+80,设这种水果每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该水果售价定为每千克多少元时,每天销售利润最大?最大利润是多少元?
(3)如果商家为“薄利多销”,规定这种水果售价每千克不高于28元,则商家要想每天获利150元的销售利润,售价应定为每千克多少元?
查看答案和解析>>
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:解答题
某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P= (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:解答题
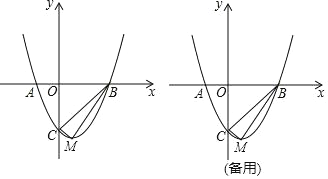
已知:如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于点C,该抛物线的顶点为M.
(1)求点A、B、C的坐标.
(2)求直线BM的函数解析式.
(3)试说明:∠CBM+∠CMB=90°.
(4)在抛物线上是否存在点P,使直线CP把△BCM分成面积相等的两部分?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2019届人教版九年级数学上册 第22章二次函数单元测试试卷 题型:解答题
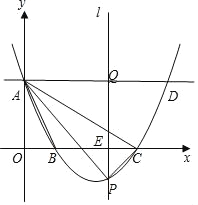
如图,在平面直角坐标系中,抛物线y= x2+bx+c与y轴的交于点A(0,3),与x轴的交于点B和C,点B的横坐标为2.点A关于抛物线对称轴对称的点为点D,在x轴上有一动点E(t,0),过点E作平行于y轴的直线与抛物线、直线AD的交点分别为P、Q.
x2+bx+c与y轴的交于点A(0,3),与x轴的交于点B和C,点B的横坐标为2.点A关于抛物线对称轴对称的点为点D,在x轴上有一动点E(t,0),过点E作平行于y轴的直线与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当点P在线段AC的下方时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似.若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com