
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:填空题
如图,长方体的长为4cm,宽为2cm,高为5cm,若用一根细线从点A开始经过4个侧面缠绕一圈到达点B,则所用细线的长度最短为__________cm.

查看答案和解析>>
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:填空题
如图,△ABC中,∠ACB=90°,AB=2,BC=AC,D为AB的中点,E为BC上一点,将△BDE沿DE翻折,得到△FDE,EF交AC于点G,则△ECG的周长是___________.

查看答案和解析>>
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
(1)计算:∣1- ∣+
∣+  -(π-3.14)0
-(π-3.14)0
(2)已知 (x-1)2 =16,求x的值
(3)已知8(x-1)3 -27=0,求x的值
查看答案和解析>>
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
如图,直线l及A、B两点(保留作图痕迹,不写作法)。
(1)如图①,在直线l上作一点P,使PA=PB;
(2)如图②,在直线l上作一点Q,使l平分∠AQB;
(3)如图③,在直线l上作一点C,使△ABC周长最短;
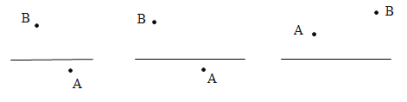
① ② ③
查看答案和解析>>
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
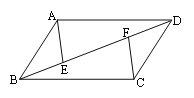
如图,四边形ABCD中,AB=CD,AB∥CD,点E、F在线段BD上,且BE=DF,连接AE、CF.
(1)指出线段AE与CF的关系,并说明理由;
(2)若将题中的条件“点E、F在线段BD上”改为“点E、F在直线BD上” ,那么(1)中的结论还一定能成立吗?若能,直接写出结论;若不能,请举出反例加以说明.
查看答案和解析>>
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
如图,△ABC中,AD是高,CE是中线,点G是CE的中点,且DG⊥CE,垂足为点G.
(1)求证:DC=BE;
(2)若∠AEC=54°,求∠BCE的度数.

查看答案和解析>>
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
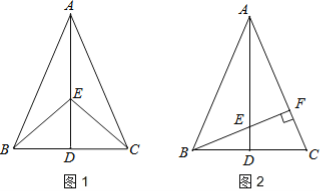
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
查看答案和解析>>
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
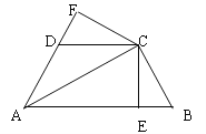
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△ACE≌△ACF;
(2)若AB=21,AD=9,AC=17,求CF的长.
查看答案和解析>>
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
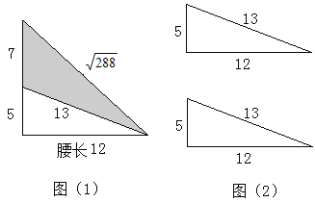
将一个边长为5、12、13的直角三角形拼上一个三角形后可以拼成一个等腰三角形,图1就是其中的一种拼法,请你画出其他所有可能的情形,并在图上标出所拼成等腰三角形的腰的长度.(选用图2中的备用图画图,每种情形用一个图形单独表示,并用①、②、③…编号,若备用图不够,请自己画图补充)
查看答案和解析>>
科目: 来源:江苏省宜兴市周铁学区2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
(问题情境)
课外兴趣小组活动时,老师提出了如下问题:
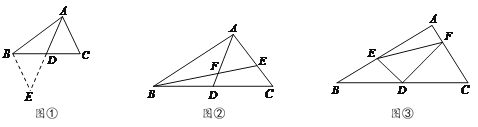
如图①,△ABC中,若AB=10,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是( ).
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(初步运用)
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4,EC=3,求线段BF的长.
(灵活运用)
如图③,在△ABC中,∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com