
科目: 来源: 题型:
【题目】已知一个口袋中装有4个只有颜色不同的球,其中3个白球,1个黑球.
(1)求从中随机抽取出一个黑球的概率是多少;
(2)若从口袋中摸出一个球,记下颜色后不放回,再摸出一个球。请列表或作出树状图,求两次都摸出白球的概率?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负。如果从A到B记为:A→B(+1,+3);从C到D记为:C→D(+1,-2)。其中第一个数表示左右方向,第二个数表示上下方向,那么图中
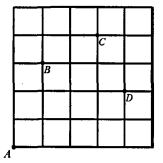
(1)A→C( , ),C→(-2, );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)假如这只甲虫从A处去甲虫P处的行走路线依次为
(+2,+2),(+1,-1),(-2,+3),请在图中标出P的位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两同学只有一张乒乓球比赛的门票,谁都想去,最后商定通过转盘游戏决定.游戏规则是:转动下面平均分成三个扇形且标有不同颜色的转盘,转盘连续转动两次,若指针前后所指颜色相同,则甲去;否则乙去.(如果指针恰好停在分割线上,那么重转一次,直到指针指向一种颜色为止)

(1)转盘连续转动两次,指针所指颜色共有几种情况?通过画树状图或列表法加以说明;
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=BC,BD=CE,M是AC边上的中点。
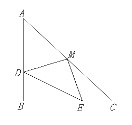
(1)求证:△DEM是等腰直角三角形.
(2)已知AD=4,CE=3,求DE的长。
查看答案和解析>>
科目: 来源: 题型:
【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折成什么几何体?________________.

(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为![]() ,顶点个数为
,顶点个数为![]() ,棱数为
,棱数为![]() ,分别计算第(1)题中两个多面体的
,分别计算第(1)题中两个多面体的![]() 的值?你发现什么规律?
的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
查看答案和解析>>
科目: 来源: 题型:
【题目】2015年9月24日台风杜鹃登陆,给我福建、浙江等地造成严重影响.为民排忧解难的解放军叔叔驾着冲锋舟沿一条东西方向的河流营救灾民,早晨从A地出发,晚上最后到达B地,约定向东为正方向,当天航行依次记录如下(单位:千米):
14,﹣9,18,﹣7,13,﹣6,10,﹣5
问:(1)B地在A地的东面,还是西面?与A地相距多少千米?
(2)这一天冲锋舟离A地最远多少千米?
(3)若冲锋舟每千米耗油0.5升,油箱容量为30升,求途中至少需要补充多少升油?
查看答案和解析>>
科目: 来源: 题型:
【题目】若干个偶数按每行8个数排成如图所示的阵列:

(1)图中方框内的9个数的和与中间的数有什么关系?
(2)小亮画了一个方框,他所画的方框内9个数的和为360,求这9个数;(直接写出答案)。
(3)小霞也画了一个方框,方框内9个数的和为262,你能写出这9个数吗?如果不能,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110,∠BOC=![]() ,将△BOC绕点C按顺时针方向旋转60得△ADC,连接OD
,将△BOC绕点C按顺时针方向旋转60得△ADC,连接OD
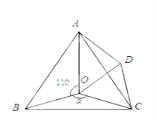
(1)△COD是什么三角形?说明理由;
(2)若AO=![]() ,AD=
,AD=![]() ,OD=
,OD=![]() (
(![]() 为大于1的整数),求
为大于1的整数),求![]() 的度数
的度数
(3)当![]() 为多少度时,△AOD是等腰三角形?
为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
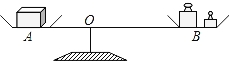
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
查看答案和解析>>
科目: 来源: 题型:
【题目】观察图,解答下列问题.

(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,……,第六层有11个圆圈.如果要你继续画下去第n层 有 圆圈
(2)某一层上有65个圆圈,这是第 层
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3 = 22.
同样,
由前三层的圆圈个数和得:1+3+5 = 32.
由前四层的圆圈个数和得:1+3+5+7 = 42.
由前五层的圆圈个数和得:1+3+5+7+9 = 52.
……
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1+3+5+…+299的和;
(5)计算:101+103+105+…+299的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com