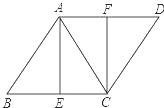
（1）求证：四边形AECF是矩形；

（2）若AB=6，求菱形的面积．

（1）该班共有多少名学生？

（2）请在图1中将“乒乓球”部分的图形补充完整；

（3）若全年级共有1200名学生，估计全年级参加乒乓球活动的学生有多少名？

（4）求出扇形统计图中表示“足球”的扇形的圆心角度数．

A. 精确到百分位 B. 精确到万分位 C. 精确到0.001 D. 精确到0.0001

A．x2+y2 B．x2﹣y C．x2+x+1 D．x2﹣2x+1

A. 9 B. －9 C. 15 D. －15

A． b（a+1）（a ﹣1） B． a（b+1）（b﹣1） C． b（a2﹣1） D． b（a﹣1）2

（1）点E、F分别是边AB、BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是 ；

（2）点E、F、P分别在线段AB、BC、AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是 ．

【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（）、面数（）、棱数（）之间存在的一个有趣的关系式，被称为欧拉公式，请你观察下列几种简单多面体模型，解答下列问题：

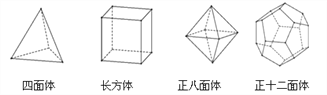
（1）根据上面多面体模型，完成表格中的空格；

（1）你发现顶点数（）、面数（）、棱数（）之间存在的关系式是_______.

（2）正十二面体有个顶点，那它有______条棱；

（3）一个多面体的面数比顶点数大，且有条棱，则这多面体的顶点数是______；

（4）某个玻璃饰品的外形是简单多面体，它的外表是由三角形和八边形两种多边形拼接而成，且有个顶点，每个顶点处都有条棱，设该多面体表面三角形的个数为个，八边形的个数为个，求的值.

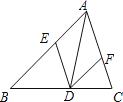
（1）如果∠BAC=90°，那么四边形AEDF是 形；

（2）如果AD是△ABC的角平分线，那么四边形AEDF是 形．

（1）求线段MN的长；

（2）若C为线段AB上任一点，满足AC+CB=a cm，其它条件不变，你能猜想MN的长度吗？并说明理由．

（3）若C在线段AB的延长线上，且满足AC﹣BC=b cm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，不要说明理由．