
科目: 来源: 题型:
【题目】下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 | 乙 | 丙 | 丁 | |
平均数(cm) | 185 | 180 | 185 | 180 |
方差 | 3. 6 | 3.6 | 7.4 | 8.1 |
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择【 】
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目: 来源: 题型:
【题目】按图填空, 并注明理由
已知: 如图, ∠1=∠2, ∠3=∠E. 求证: AD∥BE
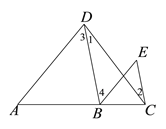
证明: ∵∠1 = ∠2 (已知)
∴ ∥ ( )
∴ ∠E = ∠ ( )
又∵ ∠E = ∠3 ( 已知 )
∴ ∠3 = ∠ ( 等量代换 )
∴ ∥ ( 内错角相等,两直线平行 )
查看答案和解析>>
科目: 来源: 题型:
【题目】某数学活动小组在一次活动中,对一个数学问题作如下探究:
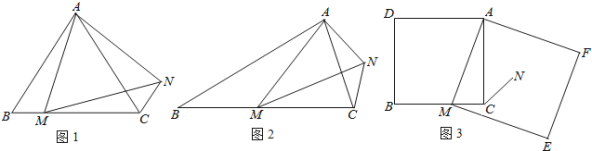
问题发现:如图1,在等边三角形ABC中,点M是边BC上任意一点,连接AM,以AM为边作等边三角形AMN,连接CN,证明:BM=CN.
变式探究:如图2,在等腰三角形ABC中,BA=BC,∠ABC=∠α,点M为边BC上任意一点,以AM为腰作等腰三角形AMN,MA=MN,使∠AMN=∠ABC,连接CN,请求出![]() 的值.(用含α的式子表示出来)
的值.(用含α的式子表示出来)
解决问题:如图3,在正方形ADBC中,点M为边BC上一点,以AM为边作正方形作AMEF,N为正方形AMEF的中心,连接CN,若正方形AMEF的边长为![]() ,CN=
,CN=![]() ,请你求正方形ADBC的边长.
,请你求正方形ADBC的边长.
查看答案和解析>>
科目: 来源: 题型:
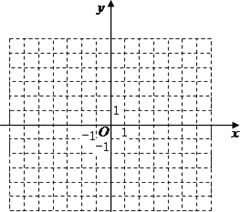
【题目】(1)在如图所示的平面直角坐标系中表示下面各点:
A(0,3);B(5,0);C(3,﹣5);D(﹣3,﹣5);E(3,5);
(2)A点到原点的距离是 .
(3)将点C向x轴的负方向平移6个单位,它与点 重合.
(4)连接CE,则直线CE与y轴是什么位置关系?
(5)点D分别到x、y轴的距离是多少?
查看答案和解析>>
科目: 来源: 题型:
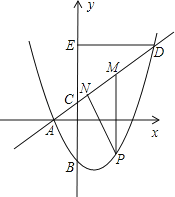
【题目】如图,抛物线y=![]() x2+bx+c与x轴交于点A(﹣2,0),交y轴于点B(0,
x2+bx+c与x轴交于点A(﹣2,0),交y轴于点B(0,![]() ).直线y=kx
).直线y=kx![]() 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.
(1)求抛物线y=![]() x2+bx+c与直线y=kx
x2+bx+c与直线y=kx![]() 的解析式;
的解析式;
(2)设点P是直线AD下方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m与x的函数关系式,并求出m的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①所示,直线L:y=m(x+10)与x轴负半轴、y轴正半轴分别交于A、B两点.

(1)当OA=OB时,试确定直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=8,BN=6,求MN的长;
(3)当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图③.
问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值?若是,请求出其值;若不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在今年的八年级期末考试中,我校(1)(2)(3)(4)班的平均分相同,方差分别为S12=20.8,S22=15.3,S32=17,S42=9.6,四个班期末成绩最稳定的是( )
A. (1)班B. (2)班C. (3)班D. (4)班
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com