
科目: 来源: 题型:
【题目】问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题

已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE.
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】(2016山东省聊城市第25题)如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】某市为提倡节约用水,采取分段收费.若每户每月用水不超过20m3 , 每立方米收费2元;若用水超过20m3 , 超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水( )m3 .
A.38
B.34
C.28
D.44
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的个数为( )
(1)用一张像底片冲出来的10张一寸照片是全等形
(2)我国国旗商店四颗小五角星是全等形
(3)所有的正六边形是全等形
(4)面积相等的两个正方形是全等形
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如果单项式x2ym+2与xny的和仍然是一个单项式,则m、n的值是( )
A.m=2,n=2
B.m=﹣1,n=2
C.m=﹣2,n=2
D.m=2,n=﹣1
查看答案和解析>>
科目: 来源: 题型:
【题目】计算:
(1) ![]() ×(-
×(-![]() );
);
(2)(-![]() )×(-
)×(-![]() );
);
(3)-2![]() ×25;
×25;
(4)(-0.3)×(-1![]() );
);
(5)-2×3×(-4);
(6)-6×(-5)×(-7);
(7)0.1×(-0.001)×(-1);
(8)(-100)×(-1)×(-3)×(-0.5);
(9)(-17)×(-49)×0×(-13)×37;
(10)(-4![]() )×1.25×(-8);
)×1.25×(-8);
(11)(-10) ×(-8.24) ×(-0.1);
(12)-![]() ×2.4×
×2.4×![]() ;
;
(13)71![]() ×(-8).
×(-8).
查看答案和解析>>
科目: 来源: 题型:
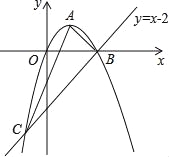
【题目】(2016广西省南宁市第24题)如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
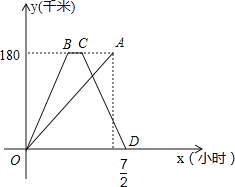
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=![]() =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com