
科目: 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目: 来源: 题型:
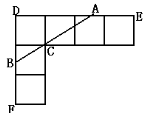
【题目】已知:正方形的边长为1.(1)如图(a),可以计算出正方形的对角线长为![]() .如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,过C作直线交DE于A,交DF于B.若DB=
.如图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如下“L”形,过C作直线交DE于A,交DF于B.若DB=![]() ,求DA的长度.
,求DA的长度.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:
①直线l外一点P到直线l的垂线段的长度,叫做点P到直线l的距离,记作d(P,l);
②两条平行线![]() ,
,![]() ,直线
,直线![]() 上任意一点到直线
上任意一点到直线![]() 的距离,叫做这两条平行线
的距离,叫做这两条平行线![]() ,
,![]() 之间的距离,记作d(
之间的距离,记作d(![]() ,
,![]() );
);
③若直线![]() ,
,![]() 相交,则定义d(
相交,则定义d(![]() ,
,![]() )=0;
)=0;
④若直线![]() ,
,![]() 重合,我们定义d(
重合,我们定义d(![]() ,
,![]() )=0,
)=0,
对于两点![]() ,
,![]() 和两条直线
和两条直线![]() ,
,![]() ,定义两点
,定义两点![]() ,
,![]() 的“
的“![]() ,
,![]() 相关距离”如下:
相关距离”如下:
d(![]() ,
,![]() |
|![]() ,
,![]() )=d(
)=d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )
)
设![]() (4,0),
(4,0),![]() (0,3),
(0,3),![]() :y=x,
:y=x,![]() :y=
:y=![]() ,
,![]() :y=kx,解决以下问题:
:y=kx,解决以下问题:
(1)d(![]() ,
,![]() |
|![]() ,
,![]() )= ;
)= ;
(2)①若k>0,则当d(![]() ,
,![]() |
|![]() ,
,![]() )最大时,k= ;
)最大时,k= ;
②若k<0,试确定k的值,使得d(![]() ,
,![]() |
|![]() ,
,![]() )最大,请说明理由.
)最大,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】(1)数学爱好者小森偶然阅读到这样一道竞赛题:
一个圆内接六边形ABCDEF,各边长度依次为 3,3,3,5,5,5,求六边形ABCDEF的面积.
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理,将六边形进行分割重组,得到图③.可以求出六边形ABCDEF的面积等于 .

(2)类比探究:一个圆内接八边形,各边长度依次为2,2,2,2,3,3,3,3.求这个八边形的面积.请你仿照小森的思考方式,求出这个八边形的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据下列条件,只能画出唯一的△ABC的是( )
A. AB=3 BC=4 B. AB=4 BC=3 ∠A=30°
C. ∠A=60°∠B=45° AB=4 D. ∠C=60°AB=5
查看答案和解析>>
科目: 来源: 题型:
【题目】把命题“等角对等边”,改写成如果___________________________________________________那么______________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】一家今年刚成立的小型快递公司业务量逐月攀升,今年7月份和9月份完成投送的快递件数分别是20万件和24.2万件.若假设该公司每月投送的快递件数的增长率相同,则这家公司投送快递件数的月平均增长率为 ________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com