
科目: 来源: 题型:
【题目】如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小.

查看答案和解析>>
科目: 来源: 题型:
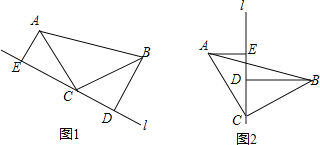
【题目】如图,△ABC中,∠ACB=90°,AC=BC,直线l过点C,BD⊥l,AE⊥l,垂足分别为D、E.
(1)当直线l不与底边AB相交时,求证:ED=AE+BD;
(2)如图2,将直线l绕点C顺时针旋转,使l与底边AB相交时,请你探究ED、AE、BD三者之间的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】永嘉县绿色和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我县收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放![]() 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为![]() 元,试写出
元,试写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
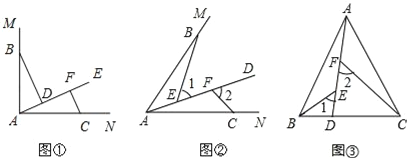
【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com