
科目: 来源: 题型:
【题目】【问题提出】
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”) 和直角三角形全等的判定方法(即“HL”) 后, 我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
不妨将问题用符号语言表示为: 在△ABC和△DEF中, AC = DF, BC = EF, ∠B =∠E,
然后, 对∠B进行分类, 可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
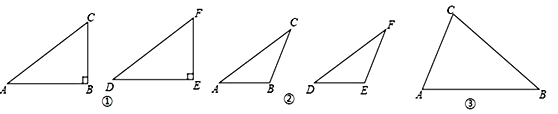
第一种情况: 当∠B是直角时, △ABC≌△DEF.
(1) 如图①, 在△ABC和△DEF, AC = DF, BC = EF, ∠B =∠E = 90°, 根据_____________, 可以知道Rt△ABC≌Rt△DEF.
第二种情况: 当∠B是钝角时, △ABC≌△DEF.
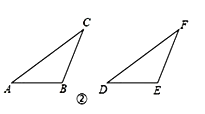
(2) 如图②, 在△ABC和△DEF, AC = DF, BC = EF, ∠B =∠E, 且∠B、∠E都是钝角.
求证: △ABC≌△DEF.
第三种情况: 当∠B是锐角时, △ABC和△DEF不一定全等.
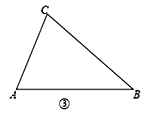
(3) 在△ABC和△DEF, AC = DF, BC = EF, ∠B = ∠E, 且∠B、∠E都是锐角, 请你用尺规在图③中作出△DEF, 使△DEF和△ABC不全等. (不写作法, 保留作图痕迹)
(4) ∠B还要满足什么条件, 就可以使△ABC≌△DEF ? 请直接写出结论: 在△ABC和△DEF中, AC = DF, BC = EF, ∠B =∠E, 且∠B、∠E都是锐角, 若__________, 则△ABC≌△DEF.
查看答案和解析>>
科目: 来源: 题型:
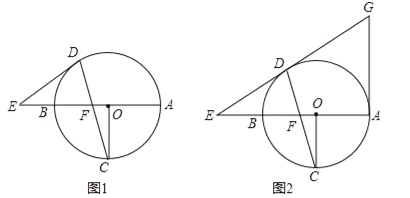
【题目】已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.
(1)如图1,求证:ED为⊙O的切线;
(2)如图2,直线ED与切线AG相交于G,且OF=1,⊙O的半径为3,求AG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】小欣同学对数据28,2■,48,50,52进行统计分析,发现其中一个两位数的个位数字被墨水污染看不到了,则分析结果与被污染数字无关的是( )
A.平均数B.方差C.中位数D.众数
查看答案和解析>>
科目: 来源: 题型:
【题目】学校有一个长为25m,宽为12m的长方体游泳池,当前水位是0.1m. 现往游泳池注水,水位每小时上升0.3m.
(1) 写出游泳池水深d(m)与注水时间x(h)的函数表达式;
(2) 如果x(h)共注水y(m3),求y与x的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为 ;若添加条件AC=EC,则可以用 公理(或定理)判定全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com