
科目: 来源: 题型:
【题目】如图,四边形ABCD是一个平行四边形,BE⊥CD于点E,BF⊥AD于点F, 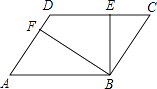
(1)请用图中表示的字母表示出平行线AD与BC之间的距离;
(2)若BE=2cm,BF=4cm,求平行线AB与CD之间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t=![]() 时,则OP= ,S△ABP= ;
时,则OP= ,S△ABP= ;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ·BP=3.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.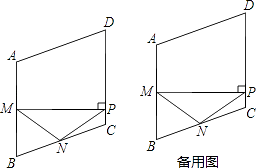
(1)若∠B=60°,这时点P与点C重合,则∠NMP=度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点. 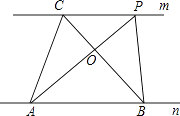
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是一个平行四边形,BE⊥CD于点E,BF⊥AD于点F, 
(1)请用图中表示的字母表示出平行线AD与BC之间的距离;
(2)若BE=2cm,BF=4cm,求平行线AB与CD之间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE. 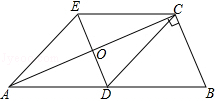
(1)求证:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时,有-1 ≤ y1 - y2 ≤ 1成立,则称这两个函数在a ≤ x ≤ b上是“相邻函数”,否则称它们在a ≤ x ≤ b上是“非相邻函数”.

例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2并研究该函数在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
(1)判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,说明理由;
(2)若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;
(3)若函数y =![]() 与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值.
与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com