
科目: 来源: 题型:
【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图1所示,求证:OB∥AC; 
(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数; 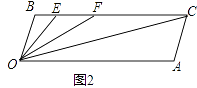
(3)在(2)的条件下,若平行移动AC,如图3,则∠OCB:∠OFB的值是 . 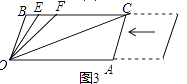
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点Q为坐标系上任意一点,某图形上的所有点在∠Q的内部(含角的边),这时我们把∠Q的最小角叫做该图形的视角.如图1,矩形ABCD,作射线OA,OB,则称∠AOB为矩形ABCD的视角.
(1)如图1,矩形ABCD,A(﹣![]() ,1),B(
,1),B(![]() ,1),C(
,1),C(![]() ,3),D(﹣
,3),D(﹣![]() ,3),直接写出视角∠AOB的度数;
,3),直接写出视角∠AOB的度数;
(2)在(1)的条件下,在射线CB上有一点Q,使得矩形ABCD的视角∠AQB=60°,求点Q的坐标;
(3)如图2,⊙P的半径为1,点P(1, ![]() ),点Q在x轴上,且⊙P的视角∠EQF的度数大于60°,若Q(a,0),求a的取值范围.
),点Q在x轴上,且⊙P的视角∠EQF的度数大于60°,若Q(a,0),求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下: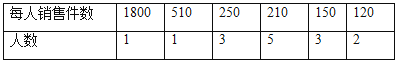
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】直线![]() 与x轴,y轴分别交于A,B两点,点A关于直线
与x轴,y轴分别交于A,B两点,点A关于直线![]() 的对称点为点C.
的对称点为点C.
(1)求点C的坐标;
(2)若抛物线![]() 经过A,B,C三点,求该抛物线的表达式;
经过A,B,C三点,求该抛物线的表达式;
(3)若抛物线![]() 经过A,B两点,且顶点在第二象限,抛物线与线段AC有两个公共点,求a的取值范围.
经过A,B两点,且顶点在第二象限,抛物线与线段AC有两个公共点,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
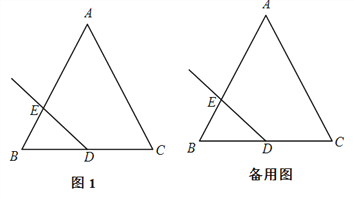
【题目】在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.
(1)依题意将图1补全;
(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF…….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.
查看答案和解析>>
科目: 来源: 题型:
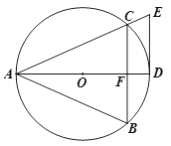
【题目】如图,⊙O为等腰三角形ABC的外接圆,AB=AC,AD是⊙O的直径,切线DE与AC的延长线相交于点E.
(1)求证:DE∥BC;
(2)若DF=n,∠BAC=2α,写出求CE长的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com