
科目: 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移4个单位长度后的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法)
(2)直接写出A′,B′,C′三点的坐标:A′(),B′(),C′().
(3)求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=![]() 的一部分.请根据图中信息解析下列问题:
的一部分.请根据图中信息解析下列问题:
(1)求y与x的函数关系式;
(2)当x=16时,大棚内的温度约为多少度?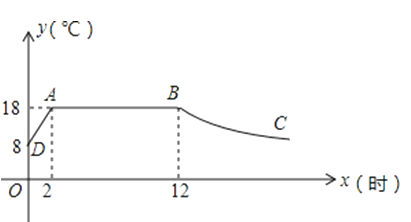
查看答案和解析>>
科目: 来源: 题型:
【题目】
【发现】
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
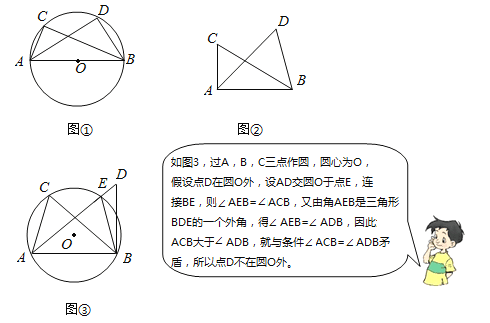
【思考】
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
请证明点D也不在⊙O内.
【应用】
利用【发现】和【思考】中的结论解决问题:若四边形ABCD中,AD∥BC,∠CAD=90°,点E在边AB上,CE⊥DE.
(1)作∠ADF=∠AED,交CA的延长线于点F(如图④),求证:DF为Rt△ACD的外接圆的切线;
(2)如图⑤,点G在BC的延长线上,∠BGE=∠BAC,已知sin∠AED=![]() ,AD=1,求DG的长.
,AD=1,求DG的长.
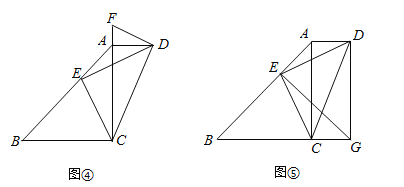
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=
,EF=![]() ,求CD的长.
,求CD的长.
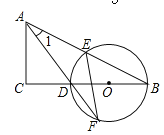
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点E,F在函数y= ![]() (x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( ) 
A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例
查看答案和解析>>
科目: 来源: 题型:
【题目】
【发现】
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)

【思考】
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
请证明点D也不在⊙O内.
【应用】
利用【发现】和【思考】中的结论解决问题:若四边形ABCD中,AD∥BC,∠CAD=90°,点E在边AB上,CE⊥DE.
(1)作∠ADF=∠AED,交CA的延长线于点F(如图④),求证:DF为Rt△ACD的外接圆的切线;
(2)如图⑤,点G在BC的延长线上,∠BGE=∠BAC,已知sin∠AED=![]() ,AD=1,求DG的长.
,AD=1,求DG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com