
科目: 来源: 题型:
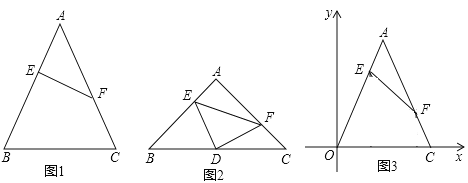
【题目】定义:如图1,等腰△ABC中,点E,F分别在腰AB,AC上,连结EF,若AE=CF,则称EF为该等腰三角形的逆等线.
(1)如图1,EF是等腰△ABC的逆等线,若EF⊥AB,AB=AC=5,AE =2,求逆等线EF的长;
(2)如图2,若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点,且点E,F分别在AB,AC上,求证:EF为等腰△ABC的逆等线;
(3)如图3,边长为6的等边三角形△AOC的边OC与X轴重合,EF是该等边三角形的逆等线.F点的坐标为(5,![]() );试求点E的坐标(若需要,本题可以直接应用结论:在直角三角形中,30°角所对的直角边等于斜边的一半.)
);试求点E的坐标(若需要,本题可以直接应用结论:在直角三角形中,30°角所对的直角边等于斜边的一半.)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.

A. 1 B. 1或3 C. 1或7 D. 3或7
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=10cm,BC=6cm,AC=8cm,BD是∠ABC的角平分线。
(1)求△ABC的面积;
(2)求△ABC的角平分线BD的长;
(3)若点E是线段AB上的一个动点,从点B以每秒2cm的速度向A运动,几秒种后△EAD是直角三角形?(此小题可直接写出答案)

查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,
(1)求证:△ABC≌△EDF;
(2)当∠CHD=120°,猜想△HDB的形状,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P. 
(1)若AE=CF; ①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间函数关系如图②所示. 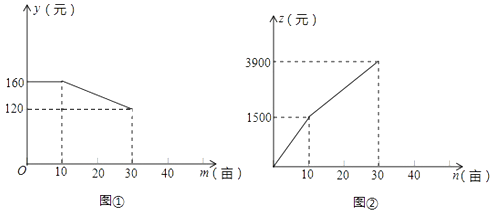
(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是元,小张应得的工资总额是元,此时,小李种植水果亩,小李应得的报酬是元;
(2)当10<n≤30时,求z与n之间的函数关系式;
(3)设农庄支付给小张和小李的总费用为w(元),当10<m≤30时,求w与m之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.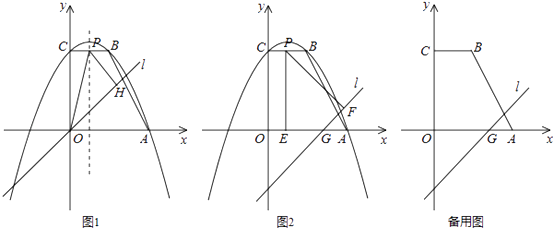
(1)求该抛物线的函数解析式;
(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】一节数学课后,老师布置了一道课后练习题:
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.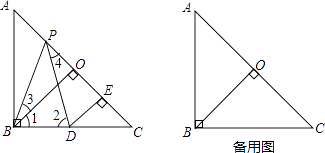
(1)理清思路完成解答
本题证明的思路可用下列框图表示: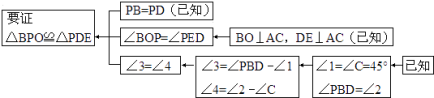
根据上述思路,请你完整地书写本题的证明过程.
(2)若PB平分∠ABO,其余条件不变.求证:AP=CD.
(3)知识迁移,探索新知
若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )
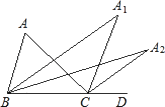
A. 19.2° B. 8° C. 6° D. 3°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com