
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG. 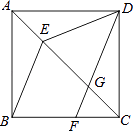
(1)求证:AE=CG;
(2)试判断BE和DF的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法,减法及乘法运算.比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求3⊕(﹣2)的值;
(2)若3⊕x的值小于16,求x的取值范围,并在数轴上表示出来.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】计算.
(1)( x-y)7÷(y-x)2÷( x-y)3;
(2) ![]() +
+![]() +
+![]() ;
;
(3)( -2)0- ![]() +
+![]() +
+![]() ·
·![]() ;
;
(4) a4m+1÷(-a) 2m+1 (m为正整数).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是定线段OA上的动点,点P从O点出发,沿线段OA运动至点A后,再立即按原路返回至点O停止,点P在运动过程中速度大小不变,以点O为圆心,线段OP长为半径作圆,则该圆的周长l与点P的运动时间t之间的函数图象大致为( )![]()
A.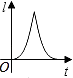
B.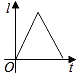
C.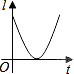
D.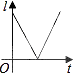
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E. 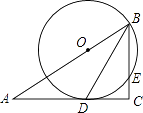
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求AD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据不等式的基本性质,把下列不等式化成“x>a”或“x<a”的形式:
(1)4x>3x+5 (2)-2x<17
(3)0.3x<-0.9 (4)x<![]() x-4
x-4
查看答案和解析>>
科目: 来源: 题型:
【题目】现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂在A、B两种不同规格的货车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元.
(1)设运送这批货物的总费用为y万元,这列货车挂A型车厢x 节,试定出用车厢节数x表示总费用y的公式.
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com