画∠AOB=90°，并画∠AOB的平分线OC．

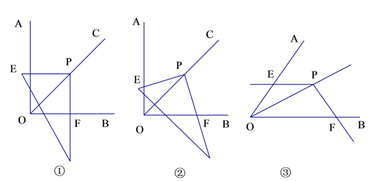
（1）把三角尺的直角顶点落在OC的任意一点P上，使三角尺的两条直角边分别与OA、OB相交于点E、F（如图①）．度量PE、PF的长度，这两条线段相等吗？

（2）把三角尺绕点P旋转（如图②），PE与PF相等吗？请说明理由.

（3）探究：画∠AOB=50°，并画∠AOB的平分线OC，在OC上任取一点P，作∠EPF=130°．∠EPF的两边分别与OA、OB相交于E、F两点（如图③），PE与PF相等吗？请说明理由.

【题目】有一个数值转换器，原理如下：
当输入的数是16时，则输出的数是 ．

【题目】如图，下列说法不正确的是（ ）
A.∠1和∠2是同旁内角
B.∠1和∠3是对顶角
C.∠3和∠4是同位角
D.∠1和∠4是内错角

【题目】如图，某日的钱塘江观潮信息如表：


按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离 （千米）与时间 （分钟）的函数关系用图3表示，其中：“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点 ，点 坐标为 ，曲线 可用二次函数 （ ， 是常数）刻画．
（1）求 的值，并求出潮头从甲地到乙地的速度；
（2）11:59时，小红骑单车从乙地出发，沿江边公路以 千米/分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？
（3）相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为 千米/分，小红逐渐落后，问小红与潮头相遇到落后潮头1.8千米共需多长时间？（潮水加速阶段速度 ， 是加速前的速度）．

（1）求证：DE∥BC；

（2）如果∠AMD=75°，求∠AGC的度数．

【题目】如图， 是 的中线， 是线段 上一点（不与点 重合）． 交 于点 ， ，连结 ．

（1）如图1，当点 与 重合时，求证：四边形 是平行四边形；
（2）如图2，当点 不与 重合时，（1）中的结论还成立吗？请说明理由.
（3）如图3，延长 交 于点 ，若 ，且 ．当 ， 时，求 的长．

（1）求∠EOB的度数；

（2）若平行移动AB，那么∠OBC∶∠OFC的值是否随之变化？若变化，找出变化规律；若不变，求出这个比值；

（3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=∠OBA？若存在，求出其度数；若不存在，说明理由。

【题目】如图是小强洗漱时的侧面示意图，洗漱台（矩形 ）靠墙摆放，高 ，宽 ，小强身高 ，下半身 ，洗漱时下半身与地面成 （ ），身体前倾成 （ ），脚与洗漱台距离 （点 ， ， ， 在同一直线上）．

（1）此时小强头部 点与地面 相距多少？
（2）小强希望他的头部 恰好在洗漱盆 的中点 的正上方，他应向前或后退多少？
（ ， ， ，结果精确到 ）

A. 0 B. 1 C. 2 D. 3

【题目】小明为了了解气温对用电量的影响，对去年自己家的每月用电量和当地气温进行了统计．当地去年每月的平均气温如图1，小明家去年月用电量如图2．
根据统计表，回答问题：

（1）当地去年月平均气温的最高值、最低值各为多少？相应月份的用电量各是多少？
（2）请简单描述月用电量与气温之间的关系；
（3）假设去年小明家用电量是所在社区家庭年用电量的中位数，据此他能否预测今年该社区的年用电量？请简要说明理由．