
科目: 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( ) 
A.b2>4ac
B.ax2+bx+c≥﹣6
C.若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目: 来源: 题型:
【题目】五张如图所示的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,按照同样的放置方式,
的长度变化时,按照同样的放置方式,![]() 始终保持不变,则
始终保持不变,则![]() ,
,![]() 满足的关系式为( )
满足的关系式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】生活常识:射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图1,MN是平面镜,若入射光线AO与水平镜面夹角为∠1,反射光线OB与水平镜面夹角为∠2,则∠1=∠2.

(1)现象解释:如图2,有两块平面镜OM,ON,且OM⊥ON,入射光线AB经过两次反射,得到反射光线CD.已知:∠1=55°,求∠4的度数.
(2)尝试探究:如图3,有两块平面镜OM,ON,入射光线AB经过两次反射,得到反射光线CD,光线AB与CD相交于点E,若∠MON=46°,求∠CEB的度数.

(3)深入思考:如图4,有两块平面镜OM,ON,且∠MON=α,入射光线AB经过两次反射,得到反射光线CD,光线AB与CD所在的直线相交于点E,∠BED=β,α与β之间满足的等量关系是 .(直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是将抛物线 ![]() 平移后得到的抛物线,其对称轴为
平移后得到的抛物线,其对称轴为 ![]() ,与x轴的一个交点为A
,与x轴的一个交点为A ![]() ,另一交点为B,与y轴交点为C.
,另一交点为B,与y轴交点为C.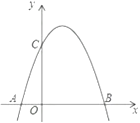
(1)求抛物线的函数表达式;
(2)若点 ![]() 为抛物线上一点,且BC⊥NC,求点N的坐标;
为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数 ![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】芳芳同学手中有一块长方形纸板和一块正方形纸板,其中长方形纸板的长为3 dm,宽为2 dm,且两块纸板的面积相等.
(1)求正方形纸板的边长(结果保留根号).
(2)芳芳能否在长方形纸板上截出两个完整的,且面积分别为2 dm2和3 dm2的正方形纸板?判断并说明理由.(提示:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90,以AC为直径作 ![]() 交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是 ![]() 的切线;
的切线;
(2)若CF=2,DF=4,求 ![]() 直径的长.
直径的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,直线a∥直线b,点A、D在直线a上,点B、C在直线b上,连接AB、AC、BD、DC,得△ABC和△BDC,△ABC的面积_______△BDC的面积(填“>”、“=”或“<”).
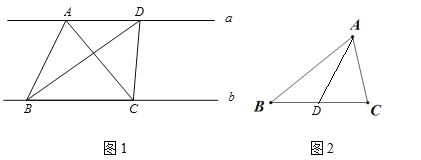

(2)如图2,已知△ABC,过点A有一条线段,将△ABC的面积平分,且交BC于点D,则![]() .
.
(3)如图3,已知四边形ABCD,请过点D作一条线段DG将四边形ABCD面积平分.
查看答案和解析>>
科目: 来源: 题型:
【题目】把下列各数分别填入相应的集合中:-(-230),![]() ,0,-0.99,1.31,5,
,0,-0.99,1.31,5,![]() ,3.14246792…,-
,3.14246792…,-![]() .
.
(1)整数集合:{ …}
(2)非正数集合:{ …}
(3)正有理数集合:{ …}
(4)无理数集合:{ …}
查看答案和解析>>
科目: 来源: 题型:
【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com