
科目: 来源: 题型:
【题目】如图在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…若点A(![]() ,0),B(0,2),则点B2018的坐标为( )
,0),B(0,2),则点B2018的坐标为( )

A. (6048,0)B. (6054,0)C. (6048,2)D. (6054,2)
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法中,①任意有理数![]() 的倒数是
的倒数是![]() ,②相反数等于自身的数只有一个,③海拔-155米表示海平面下155米,④绝对值大于本身的数一定是负数,⑤零是最小的自然数,⑥有理数包含正有理数和负有理数,⑦任意有理数
,②相反数等于自身的数只有一个,③海拔-155米表示海平面下155米,④绝对值大于本身的数一定是负数,⑤零是最小的自然数,⑥有理数包含正有理数和负有理数,⑦任意有理数![]() 的相反数是
的相反数是![]() .正确的有( )个
.正确的有( )个
A.2B.3C.4D.5
查看答案和解析>>
科目: 来源: 题型:
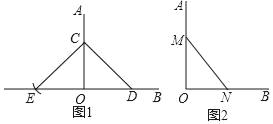
【题目】“直角”在初中数学学习中无处不在在数学活动课上,李老师要求同学们用所学知识,利用无刻度的直尺和圆规判断“已知∠AOB“是不是直角.甲、乙两名同学各自给出不同的作法,来判断∠AOB是不是直角
甲:如图1,在OA、OB上分别取点CD,以C为圆心,CD长为半径画弧,交OB的反向延长线于点E,若OE=OD,则∠AOB=90°;
乙:如图2,在OA、OB上分别截取OM=4个单位长度,ON=3个单位长度,若MN=5个单位长度,则∠AOB=90°;
甲、乙两位同学作法正确的是( )
A. 甲正确,乙不正确B. 乙正确,甲不正确
C. 甲和乙都不正确D. 甲和乙都正确
查看答案和解析>>
科目: 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:P= ,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
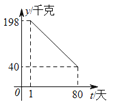
(1)求日销售量y与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
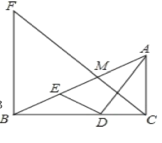
【题目】如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;②![]() ;③AC
;③AC![]() BE=12;④3BF=4AC;其中正确结论的个数有( )
BE=12;④3BF=4AC;其中正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目: 来源: 题型:
【题目】同学们都知道,![]() 表示5与
表示5与![]() 之差的绝对值,实际上也可以理解为5与
之差的绝对值,实际上也可以理解为5与![]() 两数在数轴上所对应的两点之间的距离.回答下列问题:
两数在数轴上所对应的两点之间的距离.回答下列问题:
(1)![]() _______.
_______.
(2)找出所有符合条件的整数![]() ,使得
,使得![]() 成立,这样的整数是______.
成立,这样的整数是______.
(3)对于任何有理数![]() ,
,![]() 的最小值是______.
的最小值是______.
(4)对于任何有理数![]() ,
,![]() 的最小值是_____,此时
的最小值是_____,此时![]() 的值是______.
的值是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】通过学习绝对值,我们知道![]() 的几何意义是数轴上表示数
的几何意义是数轴上表示数![]() 在数轴上的对应点与原点的距离,如:
在数轴上的对应点与原点的距离,如:![]() 表示
表示![]() 在数轴上的对应点到原点的距离.
在数轴上的对应点到原点的距离.![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离,类似的,
在数轴上对应的两点之间的距离,类似的,![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;一般地,点
在数轴上对应的两点之间的距离;一般地,点![]() ,
,![]() 在数轴上分别表示数
在数轴上分别表示数![]() 、
、![]() ,那么
,那么![]() ,
,![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
请根据绝对值的几何意义并结合数轴解答下列问题:
(1)数轴上表示![]() 和
和![]() 的两点之间的距离是___;数轴上
的两点之间的距离是___;数轴上![]() 、
、![]() 两点的距离为
两点的距离为![]() ,点
,点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数是___.
表示的数是___.
(2)点![]() ,
,![]() ,
,![]() 在数轴上分别表示数
在数轴上分别表示数![]() 、
、![]() 、
、![]() ,那么
,那么![]() 到点
到点![]() .点
.点![]() 的距离之和可表示为_ (用含绝对值的式子表示);若
的距离之和可表示为_ (用含绝对值的式子表示);若![]() 到点
到点![]() .点
.点![]() 的距离之和有最小值,则
的距离之和有最小值,则![]() 的取值范围是_ __.
的取值范围是_ __.
(3)![]() 的最小值为_ __.
的最小值为_ __.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 与点
与点![]() 是平行四边形
是平行四边形![]() 边上的动点,点
边上的动点,点![]() 以每秒
以每秒![]() 个单位长度的速度,从点
个单位长度的速度,从点![]() 运动到点
运动到点![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() →点
→点![]() →点
→点![]() 运动.当其中一个点到达终点时,另一个随之停止运动.点
运动.当其中一个点到达终点时,另一个随之停止运动.点![]() 与点
与点![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() .
.
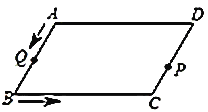
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)![]() 为何值时,将
为何值时,将![]() 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com