
科目: 来源: 题型:
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小明家的住房结构平面图,(单位:米),装修房子时,他打算将卧室以外的部分都铺上地砖,
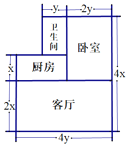
(1)若铺地砖的价格为80元/平方米,那么购买地砖需要花多少钱?(用代数式表示);
(2)已知房屋的高度为3米,现在想要在客厅和卧室的墙壁上贴上壁纸,那么需要多少平方米的壁纸(门窗所占面积忽略不计)?(用代数式表示);
(3)若x=4,y=5,且每平方米地砖的价格是90元,每平方米壁纸的价格是15元,那么,在这两项装修中,小明共要花费多少钱?(各种小的损耗不计).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.
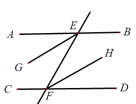
请完成以下证明过程:
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD(__________________)
∵EG平分∠AEF,FH平分∠EFD(__________)
∴∠___=![]() ∠AEF,∠___=
∠AEF,∠___= ![]() ∠EFD(____________)
∠EFD(____________)
∴∠_____=∠______(等量代换)
∴EG∥FH(__________________).
查看答案和解析>>
科目: 来源: 题型:
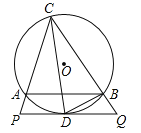
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程![]() 的两实根,且tan∠PCD=
的两实根,且tan∠PCD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连结CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
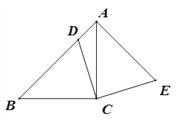
(1)求证:AB⊥AE;
(2)若![]() ,求证:四边形ADCE为正方形.
,求证:四边形ADCE为正方形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣4,4),点B的坐标为(0,2).
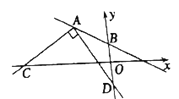
(1)求直线AB的解析式;
(2)如图,以点A为直角顶点作∠CAD=90°,射线AC交x轴于点C,射线AD交y轴于点D.当∠CAD绕着点A旋转,且点C在x轴的负半轴上,点D在y轴的负半轴上时,OC﹣OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上
与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上![]() 轴子点D,交直线AC于点E.
轴子点D,交直线AC于点E.

(1) ![]()
(2)过点P作PF⊥AC于点F.求当△PEF的周长取最大值时点P的坐标.
(3)连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求对应的P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com