
科目: 来源: 题型:
【题目】某地为了解青少年实力情况,现随机抽查了若干名初中学生进行视力情况统计,分为视力正常、轻度近视、重度近视三种情况,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:
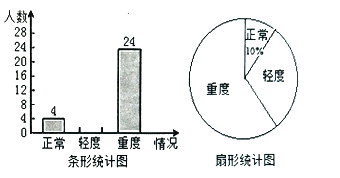
(1)求这次被抽查的学生一共有多少人?
(2)求被抽查的学生中轻度近视的学生人数,并将条形统计图补充完整;
(3)若某地有![]() 万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
万名初中生,请估计视力不正常(包括轻度近视、重度近视)的学生共有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置,PA、PB与直线MN重合,且三角板PAC、三角板PBD均可绕点P逆时针旋转.
(1)直接写出∠DPC的度数.
(2)如图②,在图①基础上,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为5°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为1°/秒,(当PA转到与PM重合时,两三角板都停止转动),在旋转过程中,当PC与PB重合时,求旋转的时间是多少?
(3)在(2)的条件下,PC、PB、PD三条射线中,当其中一条射线平分另两条射线的夹角时,请直接写出旋转的时间.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,DE//BC,∠ADE=∠EFC,将说明∠1=∠2成立的理由填写完。
解:![]() DE//BC ( )
DE//BC ( )
![]() ∠ADE=_________ ( )
∠ADE=_________ ( )
![]() ∠ADE=∠EFC ( )
∠ADE=∠EFC ( )
![]() _____________=_____________ ( )
_____________=_____________ ( )
![]() DB//EF( )
DB//EF( )
![]() ∠1= ∠2 ( )
∠1= ∠2 ( )

查看答案和解析>>
科目: 来源: 题型:
【题目】已知,关于x的一元二次方程x2+(1﹣k)x﹣k=0 (其中k为常数).
(1)判断方程根的情况并说明理由;
(2)若﹣1<k<0,设方程的两根分别为m,n(m<n),求它的两个根m和n;
(3)在(2)的条件下,若直线y=kx﹣1与x轴交于点C,x轴上另两点A(m,0)、点B(n,0),试说明是否存在k的值,使这三点中相邻两点之间的距离相等?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】高新一中初中校区名校+教育联合体主题美术展在西安高新区都市之门举办,学校组织七年级部分学生乘车参观展览,若用2辆小客车和1辆大客车,则每次可运送学生95人;若用1辆小客车和2辆大客车,则每次可运送学生115人(注意:每辆小客车和大客车都坐满).
(1)每辆小客车和大客车各能坐多少人?
(2)若现在要运送500名学生,计划租用小客车![]() 辆,大客车
辆,大客车![]() 辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案.
辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1和图2,半圆O的直径AB=4,点P(不与点A,B重合)为半圆上一点,将图形沿着BP折叠,分别得到点A,O的对称点A′,O′,设∠ABP=α.
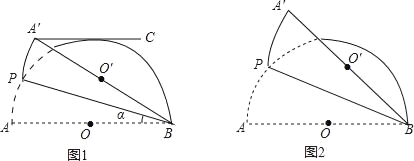
(1)如图1,当α=22.5°时,过点A′作A′C∥AB,判断A′C与半圆O的位置关系,并说明理由.
(2)如图2,当α= 时,点O′落在![]() 上.当α= 时,BA′与半圆O相切.
上.当α= 时,BA′与半圆O相切.
(3)当线段B O′与半圆O只有一个公共点B时,α的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
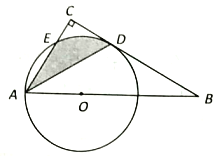
【题目】如图,点0 为Rt△ABC斜边AB上的一点,以OA 为半径的☉O与BC切于点D,与AC 交于点E,连接AD.
(1) 求证: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目: 来源: 题型:
【题目】北京时间2019年4月10日21时,人类拍摄的首张黑洞照片问世,黑洞是一种引力极大的天体,连光都逃脱不了它的束缚,数学中也存在着神奇的“黑洞数”现象:
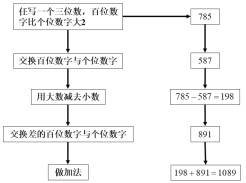
(1)请你用不同的三个数再试试,你发现了什么“神奇”的现象?
(2)请用所学过的知识现象解释一下(1)中的发现.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com