
科目: 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=![]() 的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列五个结论:
的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列五个结论:
①△CEF与△DEF的面积相等; ②△AOB∽△FOE;
③△DCE≌△CDF;④AC=BD; ⑤tan∠BAO=a
其中正确的结论是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目: 来源: 题型:
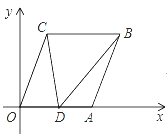
【题目】如图,已知点A(6,0),B(8,5),将线段OA平移至CB,点D(x,0)在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)求对角线AC的长;
(2)△ODC与△ABD的面积分别记为S1,S2,设S=S1﹣S2,求S关于x的函数解析式,并探究是否存在点D使S与△DBC的面积相等,如果存在,请求出x的值(或取值范围);如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(10分)如图,已知Rt△ABC中,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=6,求⊙O的半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题中,真命题有( )①同旁内角互补;②长度为2、3、5的三条线段可以构成三角形;③平方根、立方根是它本身的数是0和1;④![]() 和﹣|﹣2|互为相反数;⑤4<
和﹣|﹣2|互为相反数;⑤4<![]() <5;⑥在同一平面内,如果a∥b,a⊥c.那么b⊥c.
<5;⑥在同一平面内,如果a∥b,a⊥c.那么b⊥c.
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】将一副三角板按如图放置,则下列结论中,正确的有( )①∠1=∠3;②如果∠2=30°则有AC∥DE;③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C

A.①②③B.①②④C.③④D.①②③④
查看答案和解析>>
科目: 来源: 题型:
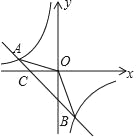
【题目】(8分)已知A(﹣4,m+10)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:
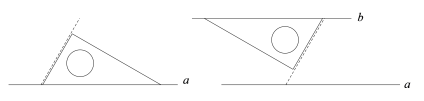
①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知矩形![]() 的边长
的边长![]() .某一时刻,动点
.某一时刻,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动;同时,动点
点匀速运动;同时,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动,问:
点匀速运动,问:

(1)经过多少时间,![]() 的面积等于矩形
的面积等于矩形![]() 面积的
面积的![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com