
科目: 来源: 题型:
【题目】如图,己知△ABC中,∠C=90°,∠A=30°,AC=![]() .动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .

查看答案和解析>>
科目: 来源: 题型:
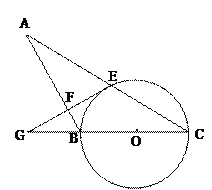
【题目】如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作EF⊥AB于点F,延长EF交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EF是⊙O的切线;
(2)若![]() ,⊙O的半径是3,求AF的长.
,⊙O的半径是3,求AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中xOy,抛物线y=x2-2(m-1)x+m2-4m+3的顶点为C,直线y=-2x+3与抛物线相交于A、B两点,点A在抛物线的对称轴的左侧.
(1)求点C的坐标(用含m的代数式表示);
(2)若P为直线OC上一动点,求△APB的面积;
(3)当OA+OB的值最小时,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】织金县某中学300名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
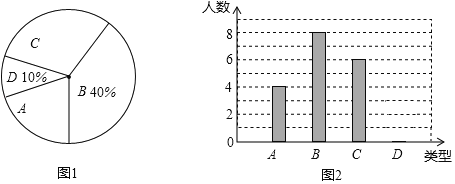
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这300名学生共植树多少棵?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等腰△ABC中,AC=BC,D在BC上,P是射线AD上一动点.
(1)如图①,若∠ACB=90°,AC=8,CD=6,当点P在线段AD上,且△PCD是等腰三角形时,求AP长.
(2)如图②,若∠ACB=90°,∠APC=45°,当点P在AD延长线上时,探究PA,PB,PC的数量关系,并说明理由.
(3)类比探究:如图③,若∠ACB=120°,∠APC=30°,当点P在AD延长线上时,请直接写出表示PA,PB,PC的数量关系的等式.

查看答案和解析>>
科目: 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )

A.4n厘米B.4m厘米C.2(m+n)厘米D.4(m+n)厘米
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目: 来源: 题型:
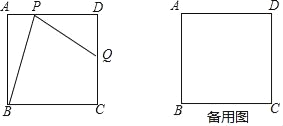
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.
(1)当QD=QC时,求∠ABP的正切值;
(2)设AP=x,CQ=y,求y关于x的函数解析式;
(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】出租车司机某天上午全是在东西走向的路上运营,如果规定向东为正,向西为负,他这天行车里程(单位:千米)如下:
-9,+5,-7,+10,+5,-8,-4,+6,-5,-4
(1)将最后一名乘客送达时,他距出发地多远?在出发地什么方向?
(2)如果每行驶1千米耗油0.4升,每升油7元,他一上午的消耗的油花费是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元![]() 的价格进了同样的60包茶叶,如果商家以每包
的价格进了同样的60包茶叶,如果商家以每包![]() 元的价格卖出这些茶叶,卖完后,这家商店( )
元的价格卖出这些茶叶,卖完后,这家商店( )
A. 盈利了B. 亏损了C. 不盈不亏D. 盈亏不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com