
科目: 来源: 题型:
【题目】随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
(1)“快车”行驶里程不超过5公里计费8元;
(2)“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
(3)A点的坐标为(6.5,10.4);
(4)从哈尔滨西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
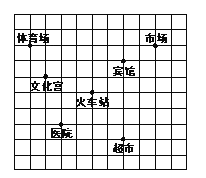
(1)请你以火车站为原点建立平面直角坐标系;
(2)写出市场、超市的坐标;
(3)请将体育场、宾馆和火车站看作三点用线段连起来,得![]() ,然后将此三角形向下平移4个单位长度,再画出平移后的
,然后将此三角形向下平移4个单位长度,再画出平移后的![]() ;
;
(4)根据坐标情况,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
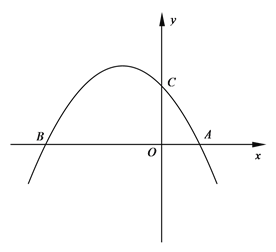
【题目】如图,二次函数y=ax2+2ax-3a的图像与x轴交于A、B两点(点A在点B的右边),与y轴交于点C.
(1)请直接写出A、B两点的坐标:A , B ;
(2)若以AB为直径的圆恰好经过这个二次函数图像的顶点.
①求这个二次函数的表达式;
②若P为二次函数图像位于第二象限部分上的一点,过点P作PQ平行于y轴,交直线BC于点Q.连接OQ、AQ,是否存在一个点P,使tan∠OQA=![]() ?如果存在,请求出点P的坐标;如果不存在,请说明理由.
?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点E是正方形ABCD的对角线BD上一点,并且AD=DE,过点E作EF⊥BD交AB于点F.
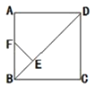
(1)求证:AF=BE,(2)若正方形的边长为1,求BF的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算;
(1)23=_____;
(2)﹣2+|﹣2|=_____;
(3)﹣6×(﹣16)=_____;
(4)![]() =_____;
=_____;
(5)2a+a=_____;
(6)![]() =_____;
=_____;
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解福清七年级学生的视力情况,现从全市七年级学生中随机抽取![]() 名学生进行调查,下列说法不正确的是一项是( )
名学生进行调查,下列说法不正确的是一项是( )
A.这种调查是抽样调查B.个体是每个学生的视力情况
C.样本容量是![]() D.若抽到的都是城区学生,则样本更具有代表性
D.若抽到的都是城区学生,则样本更具有代表性
查看答案和解析>>
科目: 来源: 题型:
【题目】某房间窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同):
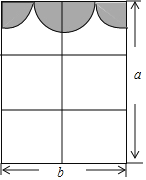
(1)装饰物所占的面积是多少?
(2)窗户中能射进阳光的部分的面积是多少?
(3)计算当a=6,b=4时,窗户中能射进阳光的部分的面积.(π取3.14)
查看答案和解析>>
科目: 来源: 题型:
【题目】某乡A,B两村盛产香梨,A村有香梨200吨,B村有香梨300吨,现将这些香梨运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的香梨为x吨,A,B两村运香梨往两仓库的运输费用分别为yA元,yB元.
(1)请填写下表,并求出yA,yB与x之间的函数关系式;
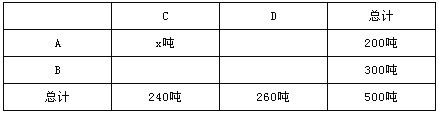
(2)当x为何值时,A村的运费较少?
(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两名同学进行登山比赛,图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶过程中,各自行进的路程随时间变化的图象,根据图象中的有关数据回答下列问题:

(1)分别求出表示甲、乙两同学登山过程中路程![]() (千米)与时间
(千米)与时间![]() (时)的函数解析式;(不要求写出自变量
(时)的函数解析式;(不要求写出自变量![]() 的取值范围)
的取值范围)
(2)当甲到达山顶时,乙行进到山路上的某点![]() 处,求
处,求![]() 点距山顶的距离;
点距山顶的距离;
(3)在(2)的条件下,设乙同学从![]() 处继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点
处继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点![]() 处与乙相遇,此时点
处与乙相遇,此时点![]() 与山顶距离为1.5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
与山顶距离为1.5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com