
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,![]() ,
,![]() .将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
.将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
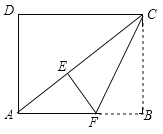
(1)求线段AC的长.
(2)求线段EF的长.
(3)点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出![]() ,并直接写出线段DH的长.
,并直接写出线段DH的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】(2016·长沙中考)若抛物线L:y=ax2+x+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系,此时,直线l叫作抛物线L的“带线”,抛物线L叫作直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=![]() 的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式.
的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】把下列各数:
﹣3.1,3.1415,﹣![]() ,+31,0.618,﹣
,+31,0.618,﹣![]() ,0,﹣1,﹣(﹣3),填在相应的集合里
,0,﹣1,﹣(﹣3),填在相应的集合里
分数集合: ;
整数集合: ;
非负整数集合: ;
正有理数集合: .
查看答案和解析>>
科目: 来源: 题型:
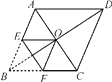
【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是“作已知角的角平分线”的尺规作图过程.
已知:如图1,∠MON.
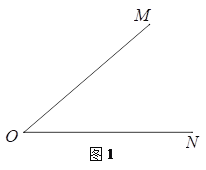
求作:射线OP,使它平分∠MON.
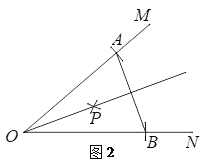
作法:如图2,
(1)以点O为圆心,任意长为半径作弧,交OM于点A,交ON于点B;
(2)连结AB;
(3)分别以点A,B为圆心,大于![]() AB的长为半径作弧,两弧相交于点P;
AB的长为半径作弧,两弧相交于点P;
(4)作射线OP.
所以,射线OP即为所求作的射线.
请回答:该尺规作图的依据是______.
查看答案和解析>>
科目: 来源: 题型:
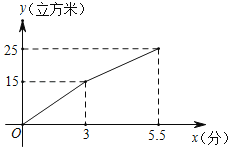
【题目】某种水泥储存罐的容量为25立方米,它有一个输入口和一个输出口.从某时刻开始,只打开输入口,匀速向储存罐内注入水泥,3分钟后,再打开输出口,匀速向运输车输出水泥,又经过2.5分钟储存罐注满,关闭输入口,保持原来的输出速度继续向运输车输出水泥,当输出的水泥总量达到8立方米时,关闭输出口.储存罐内的水泥量y(立方米)与时间x(分)之间的部分函数图象如图所示.
(1)求每分钟向储存罐内注入的水泥量.
(2)当3≤x≤5.5时,求y与x之间的函数关系式.
(3)储存罐每分钟向运输车输出的水泥量是 立方米,从打开输入口到关闭输出口共用的时间为 分钟.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() |,
|,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:(1)因为![]() ,所以
,所以![]() ______;
______;
因为![]() ,所以
,所以![]() ______;
______;
又因为![]() ,
,
所以当![]() ______时,
______时,![]() ______;
______;
或当![]() ______时,
______时,![]() ______,
______,
∴![]() ______或_______.
______或_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级学生参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下(单位:分):
七年级 88 94 90 94 84 94 99 94 99 100
八年级 84 93 88 94 93 98 93 98 97 99
整理数据:按如下分数段整理数据并补全表格:
成绩x 人数 年级 |
|
|
|
|
七年级 | 1 | 1 | 5 | 3 |
八年级 | 4 | 4 |
分析数据:补全下列表格中的统计量:
统计量 年级 | 平均数 | 中位数 | 众数 | 方差 |
七年级 | 93.6 | 94 | 24.2 | |
八年级 | 93.7 | 93 | 20.4 |
得出结论:你认为哪个年级学生“汉字听写”大赛的成绩比较好?并说明理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com