
科目: 来源: 题型:
【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?

查看答案和解析>>
科目: 来源: 题型:
【题目】已知数轴上A. B两点对应的数分别为4和2,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A.点B的距离相等,写出点P对应的数;
(2)数轴上是否存在点P,使点P到点A. 点B的距离之和为10?若存在,求出x的值;若不存在,请说明理由;
(3)若点A点B和点P(点P在原点)同时向右运动,它们的速度分别为2、1、1个长度单位/分,问:多少分钟后P点到点A点B的距离相等?(直接写出结果)
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB=AC,CD⊥BC于点C,交∠ABC的平分线于点D,AE平分∠BAC交BD于点E,过点E作EF∥BC交AC于点F,连接DF.
(1)补全图1;
(2)如图1,当∠BAC=90°时,
①求证:BE=DE;
②写出判断DF与AB的位置关系的思路(不用写出证明过程);
(3)如图2,当∠BAC=α时,直接写出α,DF,AE的关系.
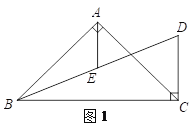
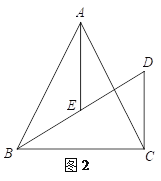
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2bx﹣3的对称轴为直线x=2.
(1)求b的值;
(2)在y轴上有一动点P(0,m),过点P作垂直y轴的直线交抛物线于点A(x1,y1),B(x2,y2),其中x1<x2.
①当x2﹣x1=3时,结合函数图象,求出m的值;
②把直线PB下方的函数图象,沿直线PB向上翻折,图象的其余部分保持不变,得到一个新的图象W,新图象W在0≤x≤5时,﹣4≤y≤4,求m的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=60°,BC=3厘米,AC=4厘米,点P从点B出发,沿B→C→A以每秒1厘米的速度匀速运动到点A.设点P的运动时间为x秒,B、P两点间的距离为y厘米.
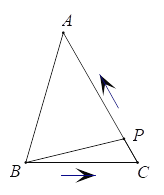
小新根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小新的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y(cm) | 0 | 1.0 | 2.0 | 3.0 | 2.7 | 2.7 | m | 3.6 |
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC中画出点P所在的位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】某家具厂生产一种餐桌和椅子,餐桌每张定价为![]() 元,椅子每把定价为
元,椅子每把定价为![]() 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:
方案一:每买一张餐桌就赠送一把椅子;
方案二:餐桌和椅子都按定价的![]() 付款.
付款.
某餐厅计划添置![]() 张餐桌和
张餐桌和![]() 把椅子.
把椅子.
(1)若![]() ,请用含
,请用含![]() 的代数式分别把两种方案的费用表示出来.
的代数式分别把两种方案的费用表示出来.
(2)已知![]() ,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,把它们分别标号1、2、3、4.小明先随机地摸出一个小球,小强再随机地摸出一个小球.记小明摸出球的标号为x,小强摸出的球标号为y.小明和小强在此基础上共同协商一个游戏规则:当x>y时小明获胜。否则小强获胜.
(1)若小明摸出的球不放回,求小明获胜的概率;
(2)若小明摸出的球放回后小强再随机摸球,问他们制定的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,动点
,动点![]() 从点
从点![]() 沿
沿![]() 以每秒
以每秒![]() 个单位的速度运动;动点
个单位的速度运动;动点![]() 从点
从点![]() 沿
沿![]() 以每秒
以每秒![]() 个单位的速度运动.
个单位的速度运动.![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() 秒.
秒.
(1)在![]() 时,
时,![]() 点坐标 ,
点坐标 ,![]() 点坐标 ;
点坐标 ;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是矩形?
是矩形?
(3)运动过程中,四边形![]() 能否为菱形?若能,求出
能否为菱形?若能,求出![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
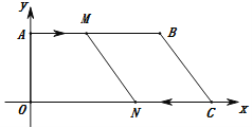
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以AB为直径作⊙O,过点A作⊙O的切线AC,连结BC,交⊙O于点D,点E是BC边的中点,连结AE.
(1)求证:∠AEB=2∠C;
(2)若AB=6,![]() ,求DE的长.
,求DE的长.
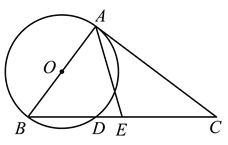
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() ,
,![]() .
.

(1)试说明![]() 成立的理由.(完成下面的填空)
成立的理由.(完成下面的填空)
证明:![]() ,
,
![]() ,(________________)
,(________________)
又![]() ,(已知)
,(已知)
![]() ,(________________)
,(________________)
![]() .(________________)
.(________________)
(2)若![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com