
科目: 来源: 题型:
【题目】探索规律,观察下面算式,解答问题.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)请猜想:1+3+5+7+9+…+19=________;
(2)请猜想:1+3+5+7+9+…+(2n-1)=________;
(3)试计算:101+103+…+197+199.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解题:
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1,依次类推,排在第n位的数称为第n项,记为an.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.
则:(1)等比数列3,6,12,…的公比q为 ,第4项是 .
(2)如果一个数列a1,a2,a3,a3,…是等比数列,且公比为q,那么根据定义可得到:
![]() ,……
,…… ![]() .
.
∴a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q= a1q3,……
由此可得:an= (用a1和q的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
查看答案和解析>>
科目: 来源: 题型:
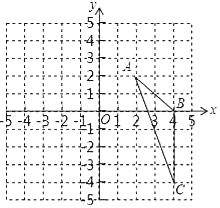
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,P为CD中点,点Q为AB上的动点(不与A,B重合).过Q作QM⊥PA于M,QN⊥PB于N.设AQ的长度为x,QM与QN的长度和为y.则能表示y与x之间的函数关系的图象大致是( )
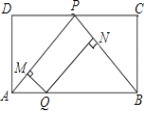

A. B. C. D.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )
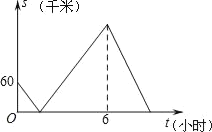
A. 货车的速度是60千米/小时
B. 离开出发地后,两车第一次相遇时,距离出发地150千米
C. 货车从出发地到终点共用时7小时
D. 客车到达终点时,两车相距180千米
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目: 来源: 题型:
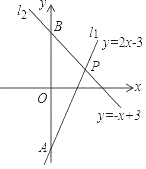
【题目】如图,已知直线l1:y=2x﹣3与直线l2:y=﹣x+3相交于点P,分别与y轴相交于点A、B.
(1)求点P的坐标;
(2)点M(0,k)为y轴上的一个动点,过点M作y轴的垂线交l1和l2于点N,Q,当NQ=2时,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如![]() .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均为整数),则有
均为整数),则有![]() .
.
![]() ,
,![]() .这样小明就找到了一种把类似
.这样小明就找到了一种把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当![]() 、
、![]() 、
、![]() 、
、![]() 均为正整数时,若
均为正整数时,若![]() ,用含
,用含![]() 、
、![]() 的式子分别表示
的式子分别表示![]() 、
、![]() ,得:
,得:![]() ,
,![]() ;
;
(2)利用所探索的结论,找一组正整数![]() 、
、![]() 、
、![]() 、
、![]() 填空:
填空: ![]()
![]()
![]()
![]()
![]() ;
;
(3)若![]() ,且
,且![]() 、
、![]() 、
、![]() 均为正整数,求
均为正整数,求![]() 的值?
的值?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图甲,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;
(3)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com