
科目: 来源: 题型:
【题目】下列说法不正确的是( )
A.因为M是线段AB的中点,所以AM=MB=![]() AB
AB
B.在线段AM延长线上取一点B,如果AB=2AM,那么点M是线段AB的中点
C.因为A,M,B在同一直线上,且AM=MB,所以M是线段AB的中点
D.因为AM=MB,所以点M是AB的中点
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,连接CE、DF,将△CBE沿CE对折,得到△CGE,延长EG交CD的延长线于点H。

(1)求证:CE⊥DF;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
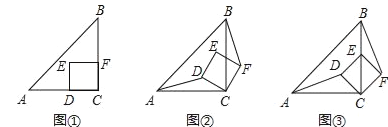
【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D、F分别在边AC、BC上,易证:AD=BF(不需要证明);
探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD、BF,其他条件不变,如图②,求证:AD=BF;
应用:若α=45°,CD=![]() ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为( )
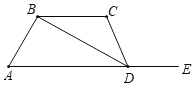
A.∠C+∠ADC=180°B.∠A+∠ABD=180°
C.∠CBD=∠ADCD.∠C=∠CDA
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=![]() .
.
(2)解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:![]() +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
+(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
查看答案和解析>>
科目: 来源: 题型:
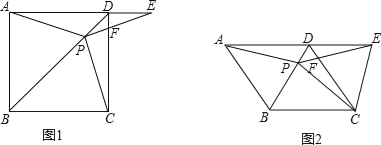
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读第①小题的计算方法,再计算第②小题.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程x2﹣2(m+1)x+m2﹣3=0.
(1)当m取何值时,方程有两个不相等的实数根?
(2)设x1、x2是方程的两根,且x12+x22=22+x1x2,求实数m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年水果大丰收,A,B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基地运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件.
(1)设从A基地运往甲销售点水果x件,总运费为W元,请用含x的代数式表示W,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com