
科目: 来源: 题型:
【题目】综合与探究
问题情境:
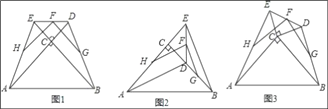
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
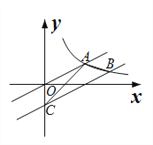
【题目】如图,已知直线![]() 与反比例函数
与反比例函数![]() (
(![]() )图像交于点A,将直线向右平移4个单位,交反比例函数
)图像交于点A,将直线向右平移4个单位,交反比例函数![]() (
(![]() )图像于点B,交y轴于点C,连结AB、AC,则△ABC的面积为_______.
)图像于点B,交y轴于点C,连结AB、AC,则△ABC的面积为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小明想利用太阳光测量楼高,发现对面墙上有这栋楼的影子,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠且高度恰好相同.此时测得墙上影子高![]() ,
,![]() ,
,![]() (点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.
(点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.

查看答案和解析>>
科目: 来源: 题型:
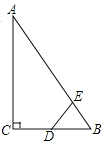
【题目】如图,Rt△ABC中,![]() ,
,![]() ,
,![]() ,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿AB向B点运动,设E点的运动时间为t秒,连接DE,当以B、D、E为顶点的三角形与△ABC相似时,t的值为( )
,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿AB向B点运动,设E点的运动时间为t秒,连接DE,当以B、D、E为顶点的三角形与△ABC相似时,t的值为( )
A.2或3.5B.2或3.2C.2或3.4D.3.2或3.4
查看答案和解析>>
科目: 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目: 来源: 题型:
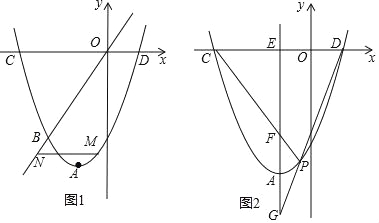
【题目】已知,在以O为原点的直角坐标系中,抛物线的顶点为A (﹣1,﹣4),且经过点B(﹣2,﹣3),与x轴分别交于C、D两点.
(1)求直线OB以及该抛物线相应的函数表达式;
(2)如图1,点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB交于点N,求MN的最大值;
(3)如图2,过点A的直线交x轴于点E,且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现:如果每件童装降价1元,那么平均可多售出2件,设每件童装降价x元(x>0)时,平均每天可盈利y元.
(1)写出y与x的函数关系式;
(2)根(1)中你写出的函数关系式,解答下列问题:
①当该专卖店每件童装降价5元时,平均每天盈利多少元?
②当该专卖店每件童装降价多少元时,平均每天盈利400元?
③该专卖店要想平均每天盈利600元,可能吗?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】在等腰Rt△ABC中,CA=BA,∠CAB=90°,点M是AB上一点,
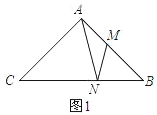
(1)点N为BC上一点,满足∠CNM=∠ANB.
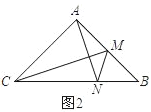
①如图1,求证:![]() ;②如图2,若点M是AB的中点,连接CM,求
;②如图2,若点M是AB的中点,连接CM,求![]() 的值;
的值;
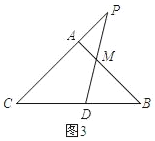
(2)如图3,若AM=1,BM=2,点P为射线CA(除点C外)上一个动点,直线PM交射线CB于点D,猜测△CPD面积是否有最小值,若有,请求出最小值:若没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com