
科目: 来源: 题型:
【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元。
(1)求文具袋和圆规的单价。
(2)学校准备购买文具袋20个,圆规若干,文具店给出两种优惠方案:
方案一:购买一个文具袋还送1个圆规。
方案二:购买圆规10个以上时,超出10个的部分按原价的八折优惠,文具袋不打折.
①设购买面规m个,则选择方案一的总费用为______,选择方案二的总费用为______.
②若学校购买圆规100个,则选择哪种方案更合算?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】将连续的奇数1、3、5、7、、,按一定规律排成如下表:

图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数
(1) 数表中从小到大排列的第9个数是17,第40个数是_________,第100个数是_________,第n个数是_________
(2) 数71排在数表的第_________行,从左往右的第_________个数
(3) 设T字框内处于中间且靠上方的数是整个数表中从小到大排列的第n个数,请你用含n的代数式表示T字框中的四个数的和
(4) 若将T字框上下左右移动,框住的四个数的和能等于406吗?如能,求出这四个数,如不能,说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.

(1)Rt△ADE与Rt△BEC全等吗?并说明理由;
(2)△CDE是不是直角三角形?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校七年级1至4班计划每班购买数量相同的图书布置班级读书角,但是由于种种原因,实际购书量与计划有出入,下表是实际购书情况:
班级 | 1班 | 2班 | 3班 | 4班 |
实际购买量(本) | a | 33 | c | 21 |
实际购买量与计划购数量的差值(本) | +12 | b | -8 | -9 |
(1) 直接写出a=__________,b=__________,c=__________
(2) 根据记录的数据可知4个班实际购书共_________本
(3) 书店给出一种优惠方案:一次购买不少于15本,其中2本书免费.若每本书售价为30元,请计算这4个班整体购书的最低总花费是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】随着人们环保意识的增强,“低碳出行”越来越为人们所倡导。小李要从家乡到宁波工作,若乘飞机需要3小时,乘汽车需要9小时。这两种交通工具每小时排放的二氧化碳总量为80千克,已知飞机每小时二氧化碳的排放量比汽车多46千克,若小李乘汽车来宁波,那么他此行与乘飞机相比将减少二氧化碳排放量多少千克?
查看答案和解析>>
科目: 来源: 题型:
【题目】探究:
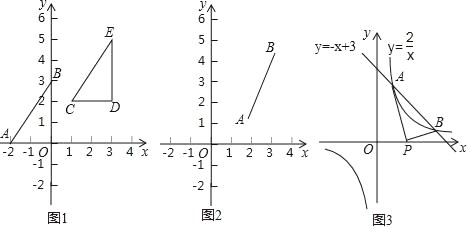
(1)图1中,已知线段AB,A(﹣2,0),B(0,3),则线段AO的长为2,BO的长为3,所以线段AB的长为;把Rt△AOB向右平移3个单位,再向上平移2个单位,得到Rt△CDE.
则Rt△CDE的顶点坐标分别为C(1,2),D(3,2),E(3,5);此时线段CD的长为 ,DE的长为 ,所以线段CE的长为 .
(2)在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB的长AB= (用含a,b,c,d的代数式表示,写出推导过程);
归纳:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d)时,线段AB的长为AB= .(不必证明)
(3)运用 在图3中,一次函数y=﹣x+3与反比例函数y=![]() 的图象交点为A,B.
的图象交点为A,B.
①求出交点A、B的坐标;
②线段AB的长;
③点P是x轴上动点,求PA+PB的最小值.
查看答案和解析>>
科目: 来源: 题型:
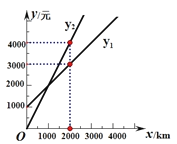
【题目】某单位急需用车,但不准备买车,他们准备和一个体车主或一国营出租车公司中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是y1元,应付给国营出租车公司的月租费是y2元, y1, y2分别与x之间的函数关系的图象(两条射线)如图所示,观察图象,回答下列问题.
(1)分别写出y1, y2与x之间的函数关系式;
(2)每月行驶的路程在什么范围内时,租国营公司的车合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣![]() 与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.
与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.
(1)求抛物线的函数表达式;
(2)若点D在第二象限且满足CD=5AC,求此时直线1的解析式;在此条件下,点E为直线1下方抛物线上的一点,求△ACE面积的最大值,并求出此时点E的坐标;
(3)如图,设P在抛物线的对称轴上,且在第二象限,到x轴的距离为4,点Q在抛物线上,若以点A,D,P,Q为顶点的四边形能否成为平行四边形?若能,请直接写出点Q的坐标;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com