练习册

  • 练习册
  • 试题
    相关习题
     0  354478  354486  354492  354496  354502  354504  354508  354514  354516  354522  354528  354532  354534  354538  354544  354546  354552  354556  354558  354562  354564  354568  354570  354572  354573  354574  354576  354577  354578  354580  354582  354586  354588  354592  354594  354598  354604  354606  354612  354616  354618  354622  354628  354634  354636  354642  354646  354648  354654  354658  354664  354672  366461 

    科目： 来源： 题型：

    【题目】完成下列推理证明．

    已知：如图，AD∥EF，∠1＝∠2.

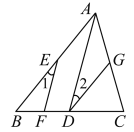
    求证：AB∥DG.

    证明：∵AD∥EF(________)，

    ∴∠1＝∠(_____)（________________）

    ∵∠1＝∠2(已知)，

    ∴∠________＝∠2(________________________)．

    ∴AB∥DG(______________________________________)

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．

    （1）求证：AE=DF；

    （2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；

    （3）当t为何值时，△DEF为直角三角形？请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，正方形ABCD 中，E，F分别是AB，BC边上的点，AF与DE相交于点G，且AF＝DE.

    求证：(1)BF＝AE；

    (2)AF⊥DE.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图．观察图中所提供的信息，解答下列问题：

    （1）汽车在前9分钟内的平均速度是多少？

    （2）汽车在中途停了多长时间？

    （3）当16≤t≤30时，求S与t的函数关系式．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知：如图，在△ABC中，AB=AC，点D为BC中点，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．求证：四边形ADCE为矩形．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，∠A=∠B=90°，E是AB上的一点，且AE=BC，∠1=∠2．求证：（1）△ADE≌△BEC （2）△CDE 是直角三角形 ．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】体育器材室有A、B两种型号的实心球，1只A型球与1只B型球的质量共7千克，3只A型球与1只B型球的质量共13千克．

    （1）每只A型球、B型球的质量分别是多少千克？

    （2）现有A型球、B型球的质量共17千克，则A型球、B型球各有多少只？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知一次函数的图象经过点A(2,0),B(0,4).

    （1）求此函数的解析式；

    （2）若点P为此一次函数图象上一动点，且△POA的面积为2，求点P的坐标.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】滴滴快车是一种便捷的出行工具，计价规则如下表：

    计费项目

    里程费

    时长费

    远途费

    单价

    1.8元/千米

    0.3元/分

    0.8元/千米

    注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算；时长费按行车的实际时间计算；远途费的收取方式为行车里程7千米以内（含7千米）不收远途费，超过7千米的，超出部分每千米收0.8元.

    （1）小王与小张各自乘坐滴滴快车，在同一地点约见，已知到达约见地点，他们的实际行车里程分别为6千米与8.5千米，两人付给滴滴快车的乘车费相同（1）求这两辆滴滴快车的实际行车时间相差多少分钟；

    （2）实际乘车时间较少的人，由于出发时间比另一人早，所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍，且比另一人的实际乘车时间的一半多8.5分钟，计算两人各自的实际乘车时间.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．

    （1）证明：AF=CE；

    （2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．

    查看答案和解析>>

    同步练习册答案