
科目: 来源: 题型:
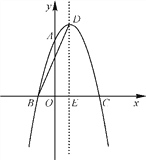
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请回答下列问题:
(1)求抛物线对应的二次函数的表达式;
(2)抛物线的顶点为D,对称轴与x轴交于点E,连接BD,求BD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=-x2+2(m-1)x+2m-m2的图象关于y轴对称,其顶点为A,与x轴两交点为B,C(B点在C点左侧).
(1)求B,C两点的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别 次数 | 购买A商品数量(件) | 购买B商品数量(件) | 消费金额(元) |
第一次 | 4 | 5 | 320 |
第二次 | 2 | 6 | 300 |
第三次 | 5 | 7 | 258 |
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买A商品多少件.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数y=x2+bx-1的图象经过点(2,3).
(1)求这个函数的表达式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)观察图象,说明y随x的增大是怎样变化的?
查看答案和解析>>
科目: 来源: 题型:
【题目】学校在“我和我的祖国”快闪拍摄活动中,为学生化妆.其中5名男生和3名女生共需化妆费190元;3名男生的化妆费用与2名女生的化妆费用相同.
(1)求每位男生和女生的化妆费分别为多少元;
(2)如果学校提供的化妆总费用为2000元,根据活动需要至少应有42名女生化妆,那么男生最多有多少人化妆.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:若A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离2倍,我们就称点C是(A,B)的美好点.
例如:如图1,点A表示的数为![]() ,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的美好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的美好点,但点D是(B,A)的美好点.
,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的美好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的美好点,但点D是(B,A)的美好点.

如图2,M,N为数轴上两点,点M所表示的数为![]() ,点N所表示的数为2.
,点N所表示的数为2.

图2
(1)点E,F,G表示的数分别是![]() ,6.5,11,其中是(M,N)美好点的是 ;写出(N,M)美好点H所表示的数是 .
,6.5,11,其中是(M,N)美好点的是 ;写出(N,M)美好点H所表示的数是 .
(2)现有一只电子蚂蚁P从点N开始出发,以2个单位每秒的速度向左运动. 当t为何值时,P,M和N中恰有一个点为其余两点的美好点?
备图
查看答案和解析>>
科目: 来源: 题型:
【题目】一只小球落在数轴上的某点P0处,第一次从P0处向右跳1个单位到P1处,第二次从P1向左跳2个单位到P2处,第三次从P2向右跳3个单位到P3处,第四次从P3向左跳4个单位到P4处…,若小球按以上规律跳了(2n+3)次时,它落在数轴上的点P2n+3处所表示的数恰好是n-3,则这只小球的初始位置点P0所表示的数是( )
A.-5B.2C.-1D.-2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线![]() 经过点B,且顶点在直线x=
经过点B,且顶点在直线x=![]() 上.
上.

(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接CD,与抛物线的对称轴交于点P,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作MN∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求出S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )

A.①②③④ B.③④ C.①③④ D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com