
科目: 来源: 题型:
【题目】已知△ABC中,点D是BC边上一点,以AD为直径的⊙O与BC相切于点D,与AD、AC分别交于点E、F.
(1)如图①,若∠AEF=52°,求∠C的度数.
(2)如图②,若EF经过点O,且∠AEF=35°,求∠B的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】找规律
如图①所示的是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间的小三角形三边的中点,得到图③,按此方法继续连接,请你根据每个图中三角形的个数的规律完成各题。

(1)将下表填写完整;
图形编号 | ① | ② | ③ | ④ | ⑤ | … |
三角形个数 | 1 | 5 | … |
(2)在第n个图形中有_________________个三角形。(用含n的式子表示)
(3)按照上述方法,能否得到2019个三角形?如果能,请求出n;如果不能,请简述理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】在A地到B地的快速通道某隧道建设,将由甲,乙两个工程队共同施工完成,据调查得知:甲,乙两队单独完成这项上程所需天数之比为4:5,若先由甲,乙两队合作40天,剩下的工程再乙队做10天完成,
(1)求甲.乙两队单独完成这取工程各需多少天?
(2)若此项工程由甲队做m天,乙队n天完成,
①请用含m的式子表示n;
②已知甲队每天的施工费为15万元,乙队每天的施工费用为10万元,若工程预算的总费用不超过1150万元,甲队工作的天数与乙队工作的天数之和不超过90天.请问甲、乙两队各工作多少天,完成此项工程总费用最少?最少费用是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】⑴先化简,再求值:已知A =2a 2-a,B = -5a+1,求当a = ![]() 时,3A-2B+1的值。
时,3A-2B+1的值。
⑵已知x = 3是方程4x-a(2-x)= 2(x-a)的解,求3a2-2a-1的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题提出):分解因式:(1)2x2+2xy﹣3x﹣3y;(2)a2﹣b2+4a﹣4b
(问题探究):某数学“探究学习”小组对以上因式分解题目进行了如下探究:
探究1:分解因式:(1)2x2+2xy﹣3x﹣3y
该多项式不能直接使用提取公因式法,公式法进行因式分解.于是仔细观察多项式的特点.甲发现该多项式前两项有公因式2x,后两项有公因式﹣3,分别把它们提出来,剩下的是相同因式(x+y),可以继续用提公因式法分解.
解:2x2+2xy﹣3x﹣3y=(2x2+2xy)﹣(3x+3y)=2x(x+y)﹣3(x+y)=(x+y)(2x﹣3)
另:乙发现该多项式的第二项和第四项含有公因式y,第一项和第三项含有公因式x,把y、x提出来,剩下的是相同因式(2x﹣3),可以继续用提公因式法分解.
解:2x2+2xy﹣3x﹣3y=(2x2﹣3x)+(2xy﹣3y)=x(2x﹣3)+y(2x﹣3)=(2x﹣3)(x+y)
探究2:分解因式:(2)a2﹣b2+4a﹣4b
该多项式亦不能直接使用提取公因式法,公式法进行因式分解,于是若将此题按探究1的方法分组,将含有a的项分在一组即a2+4a=a(a+4),含有b的项一组即﹣b2﹣4b=﹣b(b+4),但发现a(a+4)与﹣b(b+4)再没有公因式可提,无法再分解下去.于是再仔细观察发现,若先将a2﹣b2看作一组应用平方差公式,其余两项看作一组,提出公因式4,则可继续再提出因式,从而达到分解因式的目的.
解:a2﹣b2+4a﹣4b=(a2﹣b2)+(4a﹣4b)=(a+b)(a﹣b)+4(a﹣b)=(a﹣b)(4+a+b)
(方法总结):对不能直接使用提取公因式法,公式法进行分解因式的多项式,我们可考虑把被分解的多项式分成若干组,分别按“基本方法”即提取公因式法和运用公式法进行分解,然后,综合起来,再从总体上按“基本方法”继续进行分解,直到分解出最后结果.这种分解因式的方法叫做分组分解法.
分组分解法并不是一种独立的因式分解的方法,而是通过对多项式进行适当的分组,把多项式转化为可以应用“基本方法”分解的结构形式,使之具有公因式,或者符合公式的特点等,从而达到可以利用“基本方法”进行分解因式的目的.
(学以致用):尝试运用分组分解法解答下列问题:
(1)分解因式:![]()
(2)分解因式:![]()
(拓展提升):
(3)尝试运用以上思路分解因式:![]()
查看答案和解析>>
科目: 来源: 题型:
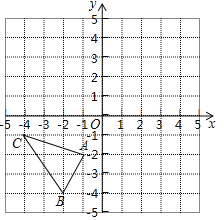
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移3个单位后得到△A1B1C1,请画出△A1B1C1并写出点B1的坐标;
(2)已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2,并直接写出直线l的函数解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】为丰富群众的业余生活并迎接社区文艺汇演,某小区特组建了一支“大妈广场舞队”(人数不超过50人).排练时,若排7排,则多3人;若排9排,且每排人数仅比排7 排时少1人,则最后-排不足6人.
(1)该“大妈广场舞队”共有多少名成员?
(2)为了提升表演效果,领队决定购买扇子和鲜花作为“大妈广场舞队”的表演道具.经预算,如果给40%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费558元;如果 给60%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费612元.问扇子和 鲜花的单价各是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com