
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD 是△ABC 的角平分线,DE,DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE.其中正确的是_________(填序号).

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
数学问题:已知![]() ,且
,且![]() ,
,![]() ,试确定
,试确定![]() 的取值范围.
的取值范围.
问题解法:![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() .①
.①
同理得![]() .②
.②
由②![]() ①得
①得![]() ,
,
![]() 的取值范围是
的取值范围是![]() .
.
完成任务:
(1)在数学问题中的条件下,写出![]() 的取值范围是_____.
的取值范围是_____.
(2)已知![]() ,且
,且![]() ,
,![]() ,试确定
,试确定![]() 的取值范围;
的取值范围;
(3)已知![]() ,
,![]() ,若
,若![]() 成立,试确定
成立,试确定![]() 的取值范围(结果用含a的式子表示).
的取值范围(结果用含a的式子表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB = 90o,AC =6,BC = 8,点F在线段AB上,以点B为圆心,BF为半径的圆交BC于点E,射线AE交圆B于点D(点D、E不重合).
(1)如果设BF = x,EF = y,求y与x之间的函数关系式,并写出它的定义域;
(2)如果![]() ,求ED的长;
,求ED的长;
(3)联结CD、BD,请判断四边形ABDC是否为直角梯形?说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图:顺次连接矩形A1B1C1D1四边的中点得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点得四边形A3B3C3D3,…,按此规律得到四边形AnBnCnDn.若矩形A1B1C1D1的面积为24,那么四边形AnBnCnDn的面积为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】某超市以每千克0.8元的价格从批发市场购进若干千克西瓜,在销售了部分西瓜之后,余下的每千克降价0.3元,直至全部售完.销售金额y与售出西瓜的千克数x之间的关系如图所示,那么超市销售这批西瓜一共赚了( )

A.20元B.32元C.35元D.36元
查看答案和解析>>
科目: 来源: 题型:
【题目】有下列等式:①由a=b,得5﹣2a=5﹣2b;②由a=b,得ac=bc;③由a=b,得![]() ;④由
;④由![]() ,得3a=2b;
,得3a=2b;
⑤由a2=b2,得a=b.其中正确的是_____.
查看答案和解析>>
科目: 来源: 题型:
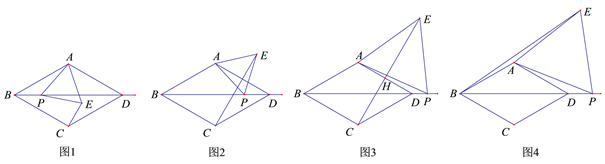
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
解:(1)如图①,延长AB到E,过点B作BF∥AC.
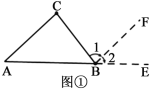
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
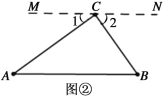
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”
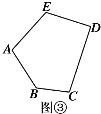
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com