
科目: 来源: 题型:
【题目】平面直角坐标系 xOy 中,定义:已知图形 W 和直线 l.如果图形 W 上存在一点 Q,使得点 Q 到直线 l 的距离小于或等于 k,则称图形 W 与直线 l“k 关联”,设图形 W:线段 AB,其中点 A(t,0)、点 B(t+2, 0).
(1)线段AB的长是 ;
(2)当t=1 时,
①已知直线y=﹣x﹣1,点A到该直线的距离为 ;
②已知直线y=﹣x+b,若线段AB与该直线“![]() 关联”,求b的取值范围。
关联”,求b的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图 1,在正方形 ABCD 中,E,F 分别是 AD,CD 上两点,BE 交 AF 于点 G,且 DE=CF.

(1)写出 BE 与 AF 之间的关系,并证明你的结论;
(2)如图 2,若 AB=2,点 E 为 AD 的中点,求 AG 的长度。
(3)在(2)的条件下,连接 GD,试证明 GD 是∠EGF 的角平分线,并求出 GD 的长;
查看答案和解析>>
科目: 来源: 题型:
【题目】露露家里新购进了一台电热水器,她对电热水器的工作原理充满好奇.查阅说明书得知,电热水器上面显示的温度为内部水箱中水的温度,每次加热前可以预设温度值,当电热水器达到预设温度后,电热水器将停止加热,开启保温功能.而在使用过程中,电热水器会自动加水,水温会下降.
露露发现电热水器中水箱的温度y(单位:℃)与接通电源后的时间x(单位:min)之间存在函数关系,她打开电热水器的开关,预设温度为70℃,并记录水温变化的情况见下表,其中在接通电源后的第8min时,电热水器达到预设温度;第18min时,妈妈开始使用电热水器.
时间x(单位:min) | 0 | 2 | 4 | 6 | 8 | 18 | 20 | 21 | 25 | 28 |
温度y(单位:℃) | 30 | 40 | 50 | 60 | 70 | 70 | 63 | m | 50.4 | 45 |
(1)m的值为_________;
(2)请在下面的坐标系中描出上表中所有数据对应的点,并根据描出的点,画出当![]() 时,温度y随时间x变化的函数图象;
时,温度y随时间x变化的函数图象;

(3)在露露的妈妈使用电热水器前,电热水器处于保温功能的时长为__________min;
(4)未加热前,电热水器的水箱中水的温度为_________℃.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)动手操作:
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点![]() 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么![]() 的度数为 。
的度数为 。
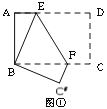
(2)观察发现:
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.

(3)实践与运用:
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小。

查看答案和解析>>
科目: 来源: 题型:
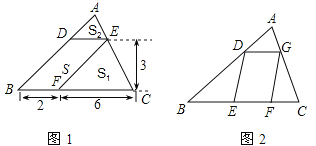
【题目】问题背景:(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F。请按图示数据填空:四边形DBFE的面积![]() ______,△EFC的面积
______,△EFC的面积![]() ______,△ADE的面积
______,△ADE的面积![]() ______。
______。
探究发现:(2)在(1)中,若![]() ,
, ![]() ,DE与BC间的距离为
,DE与BC间的距离为![]() 。请证明
。请证明![]() 。
。
拓展迁移:(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积。
查看答案和解析>>
科目: 来源: 题型:
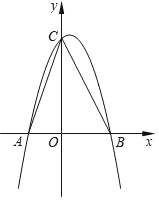
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目: 来源: 题型:
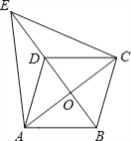
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com