
科目: 来源: 题型:
【题目】如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发向右运动,运动时间为t秒.

(1)若运动2秒时,则点P表示的数为_______,点P、Q之间的距离是______个单位;
(2)求经过多少秒后,点P、Q重合?
(3)试探究:经过多少秒后,点P、Q两点间的距离为6个单位.
查看答案和解析>>
科目: 来源: 题型:
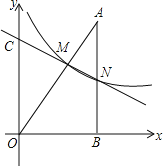
【题目】如图,在平面直角坐标系中,A点的坐标是(3,3),AB⊥x轴于点B,反比例函数y=![]() 的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM.
的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM.
(1)求反比例函数的解析式;
(2)若直线MN交y轴于点C,求△OMC的面积。
查看答案和解析>>
科目: 来源: 题型:
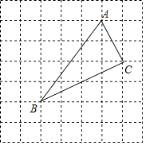
【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(1,3)、C(2,1),则点B的坐标为______;
(2)△ABC的面积为______;
(3)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AC上一点,过P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△EPD.(设AP=x)
(1)若点E落在边BC上,求AP的长;
(2)当AP为何值时,△EDB为等腰三角形.

查看答案和解析>>
科目: 来源: 题型:
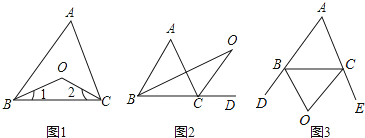
【题目】认真阅读下面关于三角形内外角平分线所夹的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+![]() ,理由如下:
,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB
∠ACB
∴∠1+∠2=![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
又∵∠ABC+∠ACB=180°-∠A
∴∠1+∠2=![]() (180°∠A)=90°
(180°∠A)=90°![]() ∠A
∠A
∴∠BOC=180°-(∠1+∠2)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A
∠A
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论:
查看答案和解析>>
科目: 来源: 题型:
【题目】设A、B、C、D为平面上任意四点,如果其中任意三点不在同一直线上,则△ABC、△ABD、△ACD、△BCD中至少存在一个三角形的某个内角满足( )
A.不超过 15°B.不超过 30°C.不超过 45°D.以上都不对
查看答案和解析>>
科目: 来源: 题型:
【题目】大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,
的小数部分我们不可能全部写出来,![]() ,于是可用
,于是可用![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是________,小数部分是________.
的整数部分是________,小数部分是________.
(2)如果![]() 的小数部分为
的小数部分为![]() ,
,![]() 的整数部分为
的整数部分为![]() ,求
,求![]() 的值.
的值.
(3)已知:![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,求
,求![]() 的相反数.
的相反数.
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是( )
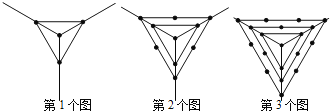
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com