
科目: 来源: 题型:
【题目】如图,直线![]() 的表达式为
的表达式为![]() ,直线
,直线![]() 与x轴交于点D,直线
与x轴交于点D,直线![]() :
:![]() 与x轴交于点A,且经过点B,直线
与x轴交于点A,且经过点B,直线![]() 、
、![]() 交于点
交于点![]() .
.
(1)求m的值;
(2)求直线![]() 的表达式;
的表达式;
(3)根据图象,直接写出![]() 的解集.
的解集.

查看答案和解析>>
科目: 来源: 题型:
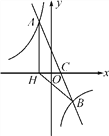
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4 ![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n).
,点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
查看答案和解析>>
科目: 来源: 题型:
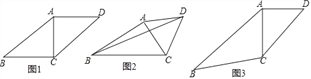
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC= ;
(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;
(3)如图3,若∠ABC=30°,∠ACD=45°,AC=2,B、D之间距离是否有最大值?如有求出最大值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,先将正方形纸片对折,折痕为EF,再把点C折叠到EF上,折痕为DN,点C在EF上的对应点为M,则下列结论中(1)AM=AB;(2)∠MCE=15°;(3)△AMD是等边三角形;(4)CN=NE,正确的个数有( )
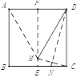
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.
(1)设该学校所买的电脑台数是x台,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别写出
元,请分别写出![]() ,
, ![]() 与x之间的关系式;
与x之间的关系式;
(2)该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?
查看答案和解析>>
科目: 来源: 题型:
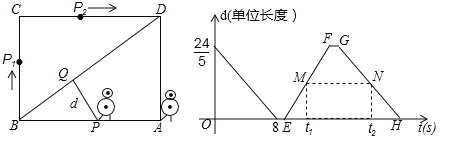
【题目】(2017江苏省苏州市)某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动.已知机器人的速度为1个单位长度/s,移动至拐角处调整方向需要1s(即在B、C处拐弯时分别用时1s).设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段 PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)求AB、BC的长;
(2)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目: 来源: 题型:
【题目】发现
如图1,在有一个“凹角∠A1A2A3”n边形A1A2A3A4……An中(n为大于3的整数),∠A1A2A3=∠A1+∠A3+∠A4+∠A5+∠A6+……+∠An﹣(n﹣4)×180°.
验证
(1)如图2,在有一个“凹角∠ABC”的四边形ABCD中,证明:∠ABC=∠A+∠C+∠D.
(2)证明3,在有一个“凹角∠ABC”的六边形ABCDEF中,证明;∠ABC=∠A+∠C+∠D+∠E+∠F﹣360°.
延伸
(3)如图4,在有两个连续“凹角A1A2A3和∠A2A3A4”的四边形A1A2A3A4……An中(n为大于4的整数),∠A1A2A3+∠A2A3A4=∠A1+∠A4+∠A5+∠A6……+∠An﹣(n﹣ )×180°.

查看答案和解析>>
科目: 来源: 题型:
【题目】若规定这样一种运算:a△b=![]() (|ab|+a+b),例如:2△3=
(|ab|+a+b),例如:2△3=![]() (|23|+2+3)=3
(|23|+2+3)=3
(1)求3△4和(-3)△(-2)的值;
(2)将1,2,3,…,50这50个自然数,任意分为25组,每组两个数,现将每组的两个数中任一数值记作a,另一个记作b,代入代数式![]() (|ab|+a+b)中进行计算,求出其结果,25组数代入后可求得25个值,求这25个值的和的最大值是_____.
(|ab|+a+b)中进行计算,求出其结果,25组数代入后可求得25个值,求这25个值的和的最大值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com