
科目: 来源: 题型:
【题目】如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
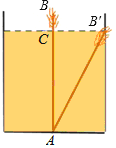
A. 15尺B. 16尺C. 17尺D. 18尺
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目: 来源: 题型:
【题目】指出下列近似数精确到哪个数位:
(1)π≈3.14 精确到______. (2)![]() 精确到____;
精确到____;
(3)21.80≈______(精确到个位);(4)579700 精确到千位是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】命题:有两个角相等的三角形是等腰三角形(简称“等角对等边”).
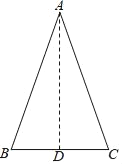
已知:如图,△ABC中,∠B=∠C.
求证:AB=AC.
三位同学作出了三种不同的辅助线,并完成了命题的证明.小刚的方法:作∠BAC的平分线AD,可证△ABD≌△ACD,得AB=AC;小亮的方法:作BC边上的高AD,可证△ABD≌△ACD,得AB=AC;小莉的方法:作BC边上的中线AD.
(1)请你写出小刚与小亮方法中△ABD≌△ACD的理由:
(2)请你按照小莉的思路完成命题的证明.
查看答案和解析>>
科目: 来源: 题型:
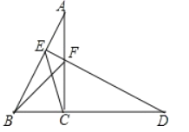
【题目】如图,把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,若直线DF垂直平分AB,垂足为点E,连接BF,CE,且BC=2,下面四个结论:①BF=![]() ;②∠CBF=45°;③△BEC的面积=△FBC的面积;④△ECD的面积为
;②∠CBF=45°;③△BEC的面积=△FBC的面积;④△ECD的面积为![]() ,其中正确的结论有( )
,其中正确的结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】全球气候变暖导致-些冰川融化并消失,在冰川|消失12年后,一种低等植物苔藓,就开始在岩石上生长,每一个苔藓都会长成近似的圆形,苔藓的直径和其生长年限近似地满足如下的关系式:d=7![]() (t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(1)计算冰川消失16年后苔藓的直径为多少厘米?
(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?
查看答案和解析>>
科目: 来源: 题型:
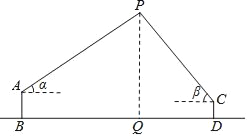
【题目】如图,爸爸和小莉在两处观测气球的仰角分别为α、β,两人的距离(BD)是200m,如果爸爸的眼睛离地面的距离(AB)为1.6m,小莉的眼睛离地面的距离(CD)为1.2m,那么气球的高度(PQ)是多少m?(用含α、β的式子表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是【A,B】的好点,但点D是【B,A】的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.

(1)数______所表示的点是【M,N】的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com