
科目: 来源: 题型:
【题目】春暖花开,市民纷纷外出踏青,某种品牌鞋专卖店抓住机遇,利用10周年店庆对其中畅销的M款运动鞋进行促销,M款运动鞋每双的成本价为800元,标价为1200元.
(1)M款运动鞋每双最多降价多少元,才能使利润率不低于20%;
(2)该店以前每周共售出M款运动鞋100双,2018年3月的一个周末,恰好是该店的10周年店庆,这个周末M款运动鞋每双在标价的基础上降价![]() m%,结果这个周末卖出的M款运动鞋的数量比原来一周卖出的M款运动鞋的数量增加了
m%,结果这个周末卖出的M款运动鞋的数量比原来一周卖出的M款运动鞋的数量增加了![]() m%,这周周末的利润达到了40000元,求m的值.
m%,这周周末的利润达到了40000元,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校计划组织全校1500名师生外出参加集体活动.经过研究,决定租用当地租车公司一共60辆![]() 、
、![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 400元 |
| 20人 | 300元 |
注:载客量指的是每辆客车最多可载该校师生的人数.
学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过22000元,一共有几种租车方案?并结合函数性质说明哪种租车方案最省钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知M=(a+24)x3﹣10x2+10x+5是关于x的二次多项式,且二次项系数和一次项系数分别为b和c,在数轴上A、B、C三点所对应的数分别是a、b、c.
![]()
(1)则a= ,b= ,c= .
(2)有一动点P从点A出发,以每秒4个单位的速度向右运动,多少秒后,P到A、B、C的距离和为40个单位?
(3)在(2)的条件下,当点P移动到点B时立即掉头,速度不变,同时点T和点Q分别从点A和点C出发,向左运动,点T的速度1个单位/秒,点Q的速度5个单位/秒,设点P、Q、T所对应的数分别是xP、xQ、xT,点Q出发的时间为t,当![]() <t<
<t<![]() 时,求2|xP﹣xT|+|xT﹣xQ|+2|xQ﹣xP|的值.
时,求2|xP﹣xT|+|xT﹣xQ|+2|xQ﹣xP|的值.
查看答案和解析>>
科目: 来源: 题型:
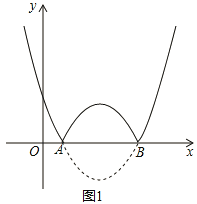
【题目】如图,抛物线![]() :
:![]() 与x轴交于A,B两点(点A在点B的左侧),将抛物线l在x轴下方部分沿x轴翻折,x轴上方的图像保持不变,就组成了函数
与x轴交于A,B两点(点A在点B的左侧),将抛物线l在x轴下方部分沿x轴翻折,x轴上方的图像保持不变,就组成了函数![]() 的图像.
的图像.
(1)若点A的坐标为(1,0).
①求抛物线![]() 的表达式,并直接写出当x为何值时,函数
的表达式,并直接写出当x为何值时,函数![]() 的值y随x的增大而增大;
的值y随x的增大而增大;
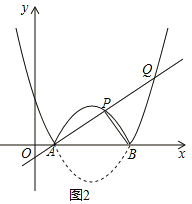
②如图2,若过A点的直线交函数![]() 的图像于另外两点P,Q,且
的图像于另外两点P,Q,且![]() ,求点P的坐标;
,求点P的坐标;
(2)当![]() 时,若函数
时,若函数![]() 的值y随x的增大而增大,直接写出h的取值范围.
的值y随x的增大而增大,直接写出h的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PAPB=kAB.

查看答案和解析>>
科目: 来源: 题型:
【题目】将若干个奇数按每行8个数排成如图的形式:
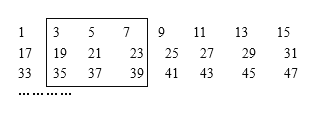
小军画了一方框框住了其中的9个数.
(1)如图中方框内9个数之和是 ;
(2)若小军画的方框内9个数之和等于333,则这个方框内左下角的那个数为_________;
(3)试说明:方框内的9个数之和总是9的倍数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点D,E分别是边BC,AC上的中点,连接DE,并延长DE至点F,使EF=ED,连接AD,AF,BF,CF,线段AD与BF相交于点O,过点D作DG⊥BF,垂足为点G.
(1)求证:四边形ABDF是平行四边形;
(2)当![]() 时,试判断四边形ADCF的形状,并说明理由;
时,试判断四边形ADCF的形状,并说明理由;
(3)若∠CBF=2∠ABF,求证:AF=2OG.

查看答案和解析>>
科目: 来源: 题型:
【题目】发现问题、探索规律,要有一双敏锐的双眼,下面的图形是由边长为1的小正方形按照某种规律排列而成的.

(1)观察图形,填写下表:
图形个数(n) | (1) | (2) | (3) |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形有 个,周长为 .
(3)写出第30个图形的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】【阅读理解】对于任意正实数a、b,因为![]() ≥0,所以
≥0,所以![]()
![]() ≥0,所以
≥0,所以![]() ≥2
≥2![]() ,只有当
,只有当![]() 时,等号成立.
时,等号成立.
【获得结论】在![]() ≥2
≥2![]() (a、b均为正实数)中,若
(a、b均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() ≥2
≥2![]() ,只有当
,只有当![]() 时,
时, ![]() 有最小值2
有最小值2![]() .
.
根据上述内容,回答下列问题:若![]() >0,只有当
>0,只有当![]() = 时,
= 时, ![]() 有最小值 .
有最小值 .
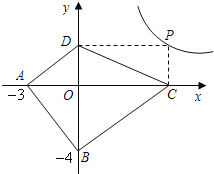
【探索应用】如图,已知A(-3,0),B(0,-4),P为双曲线![]() (
(![]() >0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
查看答案和解析>>
科目: 来源: 题型:
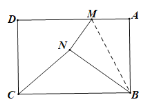
【题目】如图,矩形纸片ABCD中,AD=5,AB=3.若M为射线AD上的一个动点,将△ABM沿BM折叠得到△NBM.若△NBC是直角三角形.则所有符合条件的M点所对应的AM长度的和为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com