
科目: 来源: 题型:
【题目】在数轴上有M、N两点,M点表示的数分别为m,N点表示的数是n(n>m),则线段MN的长(点M到点N的距离)可表示为MN=n﹣m,请用上面材料中的知识解答下面的问题:一个点从数轴上的原点O开始,先向左移动3cm到达A点,再向右移动2cm到达B点,然后向右移动4cm到达C点,用1cm表示1个单位长度.
(1)请你在数轴上表示出A、B、C三点的位置,并直接写出线段AC的长度.
(2)若数轴上有一点D,且AD=4cm,则点D表示的数是什么?
(3)若将点A向右移动xcm,请用代数式表示移动后的点所表示的数.
(4)若点P以从点A向原点O移动,同时点Q以与点P相同的速度从原点O向点C移动,试探索:PQ的长是否会发生改变?如果不变,请求出PQ的长.如果改变,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个由若干个排列整齐的数组成的正方形中,图中任意一横行、一纵行及对角线的几个数之和都相等,具有这种性质的图表,称为“幻方”,中国古代称为“河图”、“洛书”,又叫“纵横图”.3阶幻方也称九宫格,即把1,2,3,4,5,6,7,8,9九个数填入3×3方格中,使每一行,每一列以及两条对角线上的数字之和都相等.请你将1,2,3,4,5,6,7,8,9填入下表的9个空格中,完成三阶幻方.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)探索发现:如图1,已知Rt△ABC中,∠ACB=90°,AC=BC,直线l过点C,过点A作AD⊥l,过点B作BE⊥l,垂足分别为D、E.求证:AD=CE,CD=BE.
(2)迁移应用:如图2,将一块等腰直角的三角板MON放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点M的坐标为(1,3),求点N的坐标.
(3)拓展应用:如图3,在平面直角坐标系内,已知直线y=﹣3x+3与y轴交于点P,与x轴交于点Q,将直线PQ绕P点沿逆时针方向旋转45°后,所得的直线交x轴于点R.求点R的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】计算
(1)(+18)+(-32)+(-16)+(+26)
(2)-![]() -(-1
-(-1![]() )-(-1
)-(-1![]() )+(-1.75)
)+(-1.75)
(3)(-42)×(![]() -
-![]() +
+![]() )
)
(4)-14-![]() [10-(3-5)2]-(-1)3
[10-(3-5)2]-(-1)3
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】小敏为了解本市的空气质量情况,从市环保局随机抽取了若干天的空气质量情况作为标本进行统计,绘制成如图所示的条形统计图和扇形统计图(部分信息为给出)
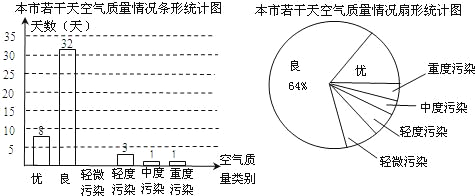
请你根据图中提供的信息,解答下列问题:
(1)本次调查中共抽取了多少天的空气质量情况作为标本?
(2)求轻微污染天数并补全条形统计图;
(3)请你估计该市这一年(365天)空气质量达到“优”和“良”的总天数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图A、O、E三点在同一条直线上,∠AOB=∠COD=90°,观察图形后有以下四个结论,其中正确的结论是( )
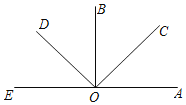
A.∠BOC=∠AOC=∠BOD
B.图中小于平角的角有6个
C.∠BOC与∠AOD互补
D.∠BOD和∠AOC互余
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并解答其后的问题:
我国古代南宋数学家秦九韶在其所著书《数学九章》中,利用“三斜求积术”十分巧妙的解决了已知三角形三边求其面积的问题,这与西方著名的“海伦公式”是完全等价的.我们也称这个公式为“海伦秦九韶公式”,该公式是:设△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,△ABC的面积为S=![]() .
.
(1)(举例应用)已知△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且a=4,b=5,c=7,则△ABC的面积为 ;
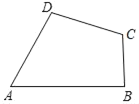
(2)(实际应用)有一块四边形的草地如图所示,现测得AB=(2![]() +4
+4![]() )m,BC=5m,CD=7m,AD=4
)m,BC=5m,CD=7m,AD=4![]() m,∠A=60°,求该块草地的面积.
m,∠A=60°,求该块草地的面积.
查看答案和解析>>
科目: 来源: 题型:
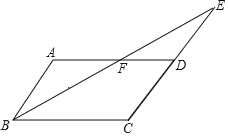
【题目】如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF,
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知数轴上有A、B、C三个点,它们表示的数分别是-24,-10,10.A、B两点间的距离记为“AB”.
![]()
(1)填空:AB= ,BC= ;
(2)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位 长度和7个单位长度的速度向右运动,设运动时间为t,用含t的代数式表示BC和AB的长,试探索:BC - AB的值是否随着时间t的变化而改变?请说明理由.
(3)现有动点P、Q都从A点出发,点P以每秒1个单位长度的速度向终点C移动;当点P 移动到B点时,点Q才从A点出发,并以每秒3个单位长度的速度向右移动,且当点P到达C点时,点Q就停止移动.设点P移动的时间为t秒,问:当t为多少时P、Q两点相距6个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com