
科目: 来源: 题型:
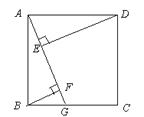
【题目】如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1) 求证:DE-BF = EF;
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时,忽然接到紧急通知:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行),试问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度应超过每小时多少千米?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
科目: 来源: 题型:
【题目】小丽剪了一些直角三角形纸片,她取出其中的几张进行了如下的操作:
操作一:如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
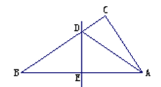
(1)如果AC=6cm,BC=8cm,试求△ACD的周长.
(2)如果∠CAD:∠BAD=4:7,求∠B的度数.
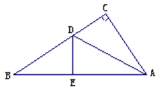
操作二:如图,小丽拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,已知两直角边AC=6cm,BC=8cm,你能求出CD的长吗?
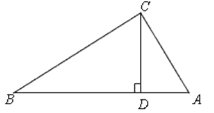
操作三:如图,小丽又拿出另一张Rt△ABC纸片,将纸片折叠,折痕CD⊥AB。你能证明:BC2+AD2=AC2+BD2吗?
查看答案和解析>>
科目: 来源: 题型:
【题目】整式乘法和乘法公式
(1)计算:(﹣x)2(2y)3
(2)化简:(a+1)2+2(a﹣1)(a+1)+(a﹣1)2
(3)如果(x+1)(x2+ax+b)的乘积中不含x2项和x项,求下面式子的值:(a+2b)(a+b)﹣2(a+b)2
(4)课本上,公式(a﹣b)2=a2﹣2ab+b2是由公式(a+b)2=a2+2ab+b2推导得出的,已知(a+b)3=a3+3a2b+3ab2+b3,则(a﹣b)3= .
查看答案和解析>>
科目: 来源: 题型:
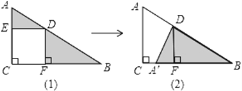
【题目】如图△ABC中有正方形EDFC,由图(1)通过三角形的旋转变换可以得到图(2).观察图形的变换方式,若AD=3,DB=4,则图(1)中△ADE和△BDF面积之和S为_____.正方形EDFC的面积为_______
查看答案和解析>>
科目: 来源: 题型:
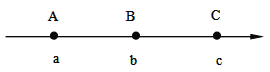
【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果![]() ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数![]() 的图象经过A(2,0),B(0,-6)两点.
的图象经过A(2,0),B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
(3)在x轴上是否存在一点P,使△ABP为等腰三角形,若存在,求出P的坐标,若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料
材料1:对称,也许是中国人最喜欢的。建筑师梁思成曾说过:“无论东方、西方,再没有一个民族对中轴对称线如此钟爱与恪守。”放眼中国的建筑,无论是宫殿、庙宇、亭台、楼阁、园林无不有着对称之美。数学世界也里有一些正整数你无论从左往右看,还是从右往左看,数字都是完全一样的,例如:11、101、2332、1234321、…,像这样的数我们叫它“对称数”.
材料2:如果一个三位数![]() ,满足a+b+c=8,我们就称这个三位数为“发财数”.
,满足a+b+c=8,我们就称这个三位数为“发财数”.
(1)请直接写出既是“对称数”又是“发财数”的所有三位数;
(2)一个三位“对称数”十位数字为7,它的各数位上的数字之和是一个自然数的平方,求这个三位数(请写出必要的推理过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com