
科目: 来源: 题型:
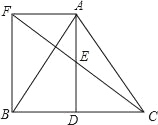
【题目】如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】将正整数1,2,3,4,5,……排列成如图所示的数阵:
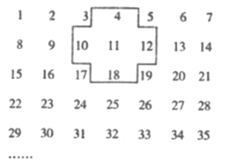
(1)十字框中五个数的和与框正中心的数11有什么关系?
(2)若将十字框上下、左右平移,可框住另外五个数,这五个数的和与框正中心的数还有这种规律吗?请说明理由;
(3)十字框中五个数的和能等于180吗?若能,请写出这五个数;若不能,请说明理由;
(4)十字框中五个数的和能等于2020吗?若能,请写出这五个数;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校9月的水费为![]() 元,电费比水费的2倍多40元,10月的水费比9月多支出了25%,电费比9月节约了25%.
元,电费比水费的2倍多40元,10月的水费比9月多支出了25%,电费比9月节约了25%.
(1)用![]() 表示该校9月的电费是多少元?
表示该校9月的电费是多少元?
(2)用![]() 表示该校10月的水、电费各是多少元?
表示该校10月的水、电费各是多少元?
(3)如果该校10月的水、电费共1130元,那么10月的水电费与9月相比超支或节约了多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】某电商在淘宝店上销售利川生产的红茶,每袋的质量标准为50![]() ,电商为了了解包装的质量状况,在同一批产品中随机抽取20袋进行检测,超过或不足的克数分别用正数或负数来表示,其记录的部分数据如下:
,电商为了了解包装的质量状况,在同一批产品中随机抽取20袋进行检测,超过或不足的克数分别用正数或负数来表示,其记录的部分数据如下:
与标准质量的差值(单位: | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
袋数 | ? | 1 | 6 | 5 | 4 | 1 | ? |
(1)已知多3![]() 的袋数是少3
的袋数是少3![]() 的袋数的2倍,求多3
的袋数的2倍,求多3![]() 的袋数和少3
的袋数和少3![]() 的袋数各是多少?
的袋数各是多少?
(2)20袋红茶的总质量与标准质量比较,共超过或不足多少![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
【题目】观察如图图形,它是按一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形十字星与五角星的个数和为7,第2个图形十字星与五角星的个数和为10,第3个图形十字星与五角星的个数和为13,按照这样的规律.则第9个图形中,十字星与五角星的个数和为( )

A.28B.29C.31D.32
查看答案和解析>>
科目: 来源: 题型:
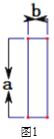
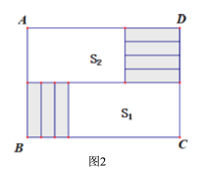
【题目】将7张相同的长方形纸片(如图1)按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分恰好可以分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=2,AD=30时,S1-S2=______.
(2)当AD=30时,用含a,b的式子表示S1-S2.
(3)若AB长度不变,AD变长,将这7张小长方形纸片按照同样的方式放在新的长方形ABCD内,而且S1-S2的值总保持不变,则a,b满足的关系是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,点A对应的数为-20,点B对应的数为120.
![]()
(1)请写出线段AB的中点C对应的数.
(2)点P从点B出发,以3个单位/秒的速度向左运动,同时点Q从点A出发,以2个单位/秒的速度向右运动,当点P、Q重合时对应的数是多少?
(3)在(2)的条件下,P、Q两点运动多长时间相距50个单位长度?
查看答案和解析>>
科目: 来源: 题型:
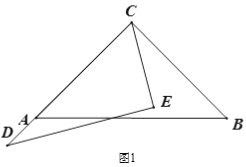
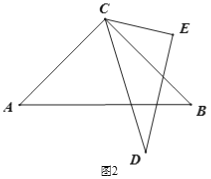
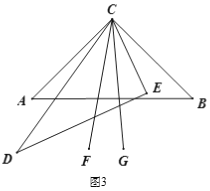
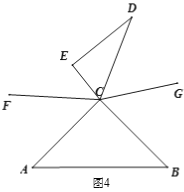
【题目】已知将一副三角板(直角三角板ABC和直角三角板CDE,∠ACB=90°,∠ECD=60°)如图1摆放,点D、A、C在一条直线上,将直角三角板CDE绕点C逆时针方向转动,变化摆放如图位置.
(1) 如图2,当∠ACD为多少度时,CB恰好平分∠ECD?
(2) 如图3,当三角板CDE摆放在∠ACB内部时,作射线CF平分∠ACE,射线CG平分∠BCD,如果三角形CDE在∠ACB内绕点C任意转动,∠FCG的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
(3) 如图4,当三角板CDE转到∠ACB外部时,射线CF、CG仍然分别平分∠ACE、∠BCD,在旋转过程中,(2)中的结论是否成立?如果结论成立,请说明理由;如果不成立,请写出你的结论并根据图4说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】把几个不同的数用大括号围起来,中间用逗号断开,如:{3,4},{-3,6,8,18},我们称之为集合,其中大括号内的数称其为集合的元素,如果一个集合满足:只要其中有一个元素a,使得-2a+4也是这个集合的元素,这样的集合我们称为条件集合,例如:集合{3,2},因为-2×3+4=-2,-2恰好是这个集合的元素,所以{3,-2}是条件集合:例如:集合{-2,9,8},因为-2×(-2)+4=8,8恰好是这个集合的元素,所以{-2,9,8}是条件集合.
(1)集合{-4,12}______条件集合;集合{![]() ,-
,-![]() ,
,![]() }______条件集合 (填“是”或“不是”)
}______条件集合 (填“是”或“不是”)
(2)若集合{8,10,n}是条件集合,求n的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com