
科目: 来源: 题型:
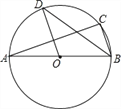
【题目】如图,AB是 圆O的直径,OB=3,BC是圆 O的弦,∠ABC的平分线交圆 O于点 D,连接OD,若∠BAC=20°,弧AD的长等于_______.
查看答案和解析>>
科目: 来源: 题型:
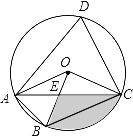
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,∠AOB=![]() ∠COB,⊙O的半径为
∠COB,⊙O的半径为![]() ,连接AC交OB于点E,OB与AC相交于点E,则图中阴影部分面积是( )
,连接AC交OB于点E,OB与AC相交于点E,则图中阴影部分面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某车行经销的A型自行车去年6月份销售总额为1.6万元,今年由于改造升级每辆车售价比去年增加200元,今年6月份与去年同期相比,销售数量相同,销售总额增加25%.
今年A,B两种型号车的进价和售价如下表:
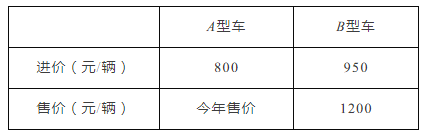
(1)求今年A型车每辆售价多少元?
(2)该车行计划7月份用不超过4.3万元的资金新进一批A型车和B型车共50辆,应如何进货才能使这批车售完后获利最多?
查看答案和解析>>
科目: 来源: 题型:
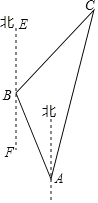
【题目】为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查.如图,一测量船在A岛测得B岛在北偏西30方向,C岛在北偏东15方向,航行100海里到达B岛,在B岛测得C岛在北偏东45,则A,C两岛的距离是 (结果保留到整数![]()
![]() )( )
)( )
A. 191海里 B. 192海里 C. 193海里 D. 194海里
查看答案和解析>>
科目: 来源: 题型:
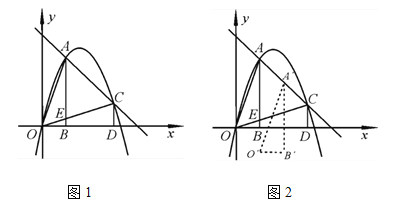
【题目】如图1,已知抛物线y=ax2+bx上有两点A、C,分别过A、C作x轴的垂线,垂足分别为点B、点D,OC与AB相交于点E.已知点A(1,3),且△AOB≌△OCD.
(1)求此抛物线的解析式;
(2)点P为线段OC上一动点,过点P作x轴的垂线交抛物线于点F,当四边形AEPF为平行四边形时,求点P坐标;
(3)如图2,若△AOB沿AC方向由A→C平移得到△A′O′B′,在平移过程中,△AOB与△OCD的重叠部分的面积记为S,试探究S是否存在最大值?若存在,求出A′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
科目: 来源: 题型:
【题目】在2018春季环境整治活动中,某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y关于x的函数关系式;
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC=2![]() ,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
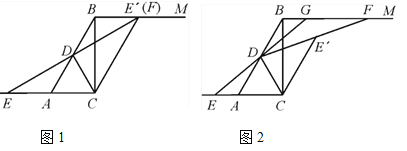
(1)如图1,当点E′与点F重合时,求证:四边形ABE′C为平行四边形;
(2)如图2,延长ED交线段BF于点G.
①设BG=x,GF=y,求y与x的函数关系式;
②若△DFG的面积为3![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0.
(1)试判断原方程根的情况;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.
(友情提示:AB=|x2﹣x1|)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com