
科目: 来源: 题型:
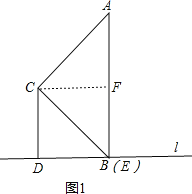
【题目】在△ABC中,∠ACB=90°,经过点B的直线l(不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、点A作直线l的垂线,垂足分别为点D、点E.
(1)如图1,当点E与点B重合时,若AE=4,判断以C点为圆心CD长为半径的圆C与直线AB的位置关系并说明理由;
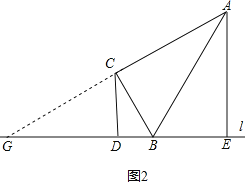
(2)如图2,当点E在DB延长线上时,求证:AE=2CD;
(3)记直线CE与直线AB相交于点F,若,![]() ,CD=4,求BD的长.
,CD=4,求BD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】直线![]() 与x轴,y轴分别交于A,B两点,点A关于直线
与x轴,y轴分别交于A,B两点,点A关于直线![]() 的对称点为点C.
的对称点为点C.
(1)求点C的坐标;
(2)若抛物线![]() 经过A,B,C三点,求该抛物线的表达式;
经过A,B,C三点,求该抛物线的表达式;
(3)若抛物线![]() 经过A,B两点,且顶点在第二象限,抛物线与线段AC有两个公共点,求a的取值范围.
经过A,B两点,且顶点在第二象限,抛物线与线段AC有两个公共点,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是最大的负整数,
是最大的负整数,![]() 是
是![]() 的倒数,
的倒数,![]() 比
比![]() 小1,且
小1,且![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 在数轴上对应的数.若动点
在数轴上对应的数.若动点![]() 从点
从点![]() 出发沿数轴正方向运动,动点
出发沿数轴正方向运动,动点![]() 同时从点
同时从点![]() 出发沿数轴负方向运动,点
出发沿数轴负方向运动,点![]() 的速度是每秒3个单位长度,点
的速度是每秒3个单位长度,点![]() 的速度是每秒1个单位长度.
的速度是每秒1个单位长度.
![]()
(1)在数轴上标出点![]() 、
、![]() 、
、![]() 的位置;
的位置;
(2)运动前![]() 、
、![]() 两点之间的距离为 ;运动t秒后,点
两点之间的距离为 ;运动t秒后,点![]() ,点
,点![]() 运动的路程分别为 和 ;
运动的路程分别为 和 ;
(3)求运动几秒后,点![]() 与点
与点![]() 相遇?
相遇?
(4)在数轴上找一点![]() ,使点
,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和等于11,直接写出所有点
三点的距离之和等于11,直接写出所有点![]() 对应的数.
对应的数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2,(这里规定:线段是面积为0的三角形)
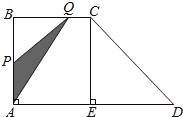
解答下列问题:
(1)当x=2s时,y= cm2;当x=![]() s时,y= cm2.
s时,y= cm2.
(2)当5≤x≤14 时,求y与x之间的函数关系式.
(3)当动点P在线段BC上运动时,求出![]() 时x的值.
时x的值.
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC=4cm,将△ABC沿CA方向平移4cm得到△EFA,连接BE,BF;BE与AF交于点G
(1)判断BE与AF的位置关系,并说明理由;
(2)若∠BEC=15°,求四边形BCEF的面积.

查看答案和解析>>
科目: 来源: 题型:
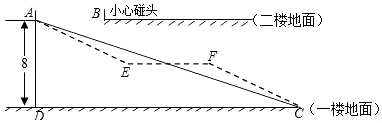
【题目】某大型购物商场在一楼和二楼之间安装自动扶梯AC,截面如图所示,一楼和二楼地面平行(即AB所在的直线与CD平行),层高AD为8米,∠ACD=20°,为使得顾客乘坐自动扶梯时不至于碰头,A、B之间必须达到一定的距离.
(1)要使身高2.26米的姚明乘坐自动扶梯时不碰头,那么A、B之间的距离至少要多少米?(精确到0.1米)
(2)如果自动扶梯改为由AE、EF、FC三段组成(如图中虚线所示),中间段EF为平台(即EF∥DC),AE段和FC段的坡度i=1:2,求平台EF的长度.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目: 来源: 题型:
【题目】图①②③是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.

(1)图①中△MON的面积=________;
(2)在图②③中以格点为顶点画出一个正方形ABCD,使正方形ABCD的面积等于(1)中△MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD的面积没有剩余(在图②、图③中画出的图形不能是全等形)
查看答案和解析>>
科目: 来源: 题型:
【题目】出租车司机王师傅某天上午的营运全是在经十路上进行的,如果规定向东为正,向西为负,他这天上午所接十位乘客的行车里程(单位:千米)如下:
+5、-2、+5、-1、+10、-3、-2、+12、+4、-5.
(1)王师傅这天上午的出发地记为0,他将最后一名乘客送抵目的地时,距上午的出发地有多远?
(2)若出租车消耗天然气量为0.1立方米/千米,这天上午王师傅共耗天然气多少立方米?
(3)若出租车起步价为9元,起步里程为3千米(包括3千米),超过部分(不足1千米按1千米计算)每千米1.5元,这天上午王师傅共得车费多少元?
查看答案和解析>>
科目: 来源: 题型:
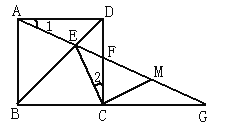
【题目】如图,正方形ABCD中,E是BD上一点,AE的延长线交CD于F,交BC的延长线于G,M是FG的中点.
(1)求证:① ∠1=∠2;② EC⊥MC.
(2)试问当∠1等于多少度时,△ECG为等腰三角形?请说明理由.
【答案】(1)①证明见解析;②证明见解析;(2)当∠1=30°时,△ECG为等腰三角形. 理由见解析.
【解析】试题分析:(1)①根据正方形的对角线平分一组对角可得![]() 然后利用边角边定理证明
然后利用边角边定理证明![]() ≌
≌![]() 再根据全等三角形对应角相等即可证明;
再根据全等三角形对应角相等即可证明;
②根据两直线平行,内错角相等可得![]() 再根据直角三角形斜边上的中线等于斜边的一半可得
再根据直角三角形斜边上的中线等于斜边的一半可得![]() 然后据等边对等角的性质得到
然后据等边对等角的性质得到![]() ,所以
,所以![]() 然后根据
然后根据![]() 即可证明
即可证明![]() 从而得证;
从而得证;
(2)根据(1)的结论,结合等腰三角形两底角相等![]() 然后利用三角形的内角和定理列式进行计算即可求解.
然后利用三角形的内角和定理列式进行计算即可求解.
试题解析:(1)证明:①∵四边形ABCD是正方形,
∴∠ADE=∠CDE,AD=CD,
在△ADE与△CDE,
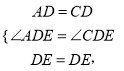
∴△ADE≌△CDE(SAS),
∴∠1=∠2,
②∵AD∥BG(正方形的对边平行),
∴∠1=∠G,
∵M是FG的中点,
∴MC=MG=MF,
∴∠G=∠MCG,
又∵∠1=∠2,
∴∠2=∠MCG,
∵![]()
∴![]()
∴EC⊥MC;
(2)当∠1=30°时, ![]() 为等腰三角形. 理由如下:
为等腰三角形. 理由如下:
∵![]() 要使
要使![]() 为等腰三角形,必有
为等腰三角形,必有![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴∠1=30°.
【题型】解答题
【结束】
24
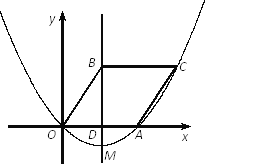
【题目】如图,已知抛物线经过原点O和点A,点B(2,3)是该抛物线对称轴上一点,过点B作BC∥x轴交抛物线于点C,连结BO、CA,若四边形OACB是平行四边形.
(1)① 直接写出A、C两点的坐标;② 求这条抛物线的函数关系式;
(2)设该抛物线的顶点为M,试在线段AC上找出这样的点P,使得△PBM是以BM为底边的等腰三角形并求出此时点P的坐标;
(3)经过点M的直线把□ OACB的面积分为1:3两部分,求这条直线的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com