
科目: 来源: 题型:
【题目】[背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b;线段AB的中点M表示的数为![]() .
.
[问题情境]
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
![]()
[综合运用]
(1)运动开始前,A、B两点的距离为 ;线段AB的中点M所表示的数 .
(2)点A运动t秒后所在位置的点表示的数为 ;点B运动t秒后所在位置的点表示的数为 ;(用含t的代数式表示)
(3)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(4)若A,B按上述方式继续运动下去,线段AB的中点M能否与原点重合?若能,求出运动时间,并直接写出中点M的运动方向和运动速度;若不能,请说明理由.(当A,B两点重合,则中点M也与A,B两点重合)
查看答案和解析>>
科目: 来源: 题型:
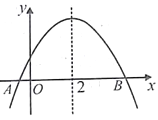
【题目】如图,已知二次函数![]() 图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )
图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )
A. ①,② B. ②,③ C. ③,④ D. ②,④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正比例函数![]() 的图象经过点(3,-6).
的图象经过点(3,-6).
(1)求这个函数的表达式;
(2)在如图所示的直角坐标系中画出这个函数的图象;
(3)判断点A(4,-2)、B(-1.5,3)是否在这个函数的图象上.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,AB=2AD,DE平分∠ADC,交AB于点E,交CB的延长线于点F,EG∥AD交DC于点G.
中,AB=2AD,DE平分∠ADC,交AB于点E,交CB的延长线于点F,EG∥AD交DC于点G.
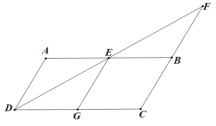
⑴求证:四边形AEGD为菱形;
⑵若![]() ,AD=2,求DF的长.
,AD=2,求DF的长.
查看答案和解析>>
科目: 来源: 题型:
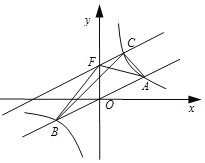
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 向上平移
向上平移![]() 个单位,交双曲线
个单位,交双曲线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积是
的面积是![]() .给出以下结论:(1)
.给出以下结论:(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .其中正确的结论有
.其中正确的结论有![]()
![]()
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如果10b=n,那么称b为n的劳格数,记为b=d(n).
(1)根据劳格数的定义,可知:d(10)=1,d(102)=2,那么:d(103)= .
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)=d(m)+d(n); d(![]() )=d(m)﹣d(n).若d(3)=0.48,d(2)=0.3,根据运算性质,填空:d(6)= ,则d(
)=d(m)﹣d(n).若d(3)=0.48,d(2)=0.3,根据运算性质,填空:d(6)= ,则d(![]() )= ,d(
)= ,d(![]() )= .
)= .
查看答案和解析>>
科目: 来源: 题型:
【题目】七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现有甲、乙两家商店出售两种同样的笔记本和钢笔.他们的定价相同:笔记本定价为每本25元,钢笔每支定价6元,但是他们的优惠方案不同,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.已知七年级需笔记本20本,钢笔x支(大于20支).问:
(1)在甲店购买需付款 元,在乙店购买需付款 元;
(2)若x=30,通过计算说明此时到哪家商店购买较为合算?
(3)当x=40时,请设计一种方案,使购买最省钱?算出此时需要付款多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价 | 40 | 90 |
售价 | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
![]() 写出y关于x的函数关系式:
写出y关于x的函数关系式:
![]() 该商品计划最多投入8000元用于购买者两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
该商品计划最多投入8000元用于购买者两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
![]() 实际进货时,生产厂家对甲种商品的出厂价下调a元
实际进货时,生产厂家对甲种商品的出厂价下调a元![]() 出售
出售![]() 且限定商场最多购购进甲种商品60件,若商场保持同种商品的售价不变,请你根据以上信息及
且限定商场最多购购进甲种商品60件,若商场保持同种商品的售价不变,请你根据以上信息及![]() 中条件,设计出使该商场获得最大利润的进货方案.
中条件,设计出使该商场获得最大利润的进货方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明在研究数学问题时遇到一个定义:将三个已经排好顺序的数:![]() ,
,![]() ,
,![]() ,称为数列
,称为数列![]() ,
,![]() ,
,![]() .计算
.计算![]() ,
,![]() ,
,![]() ,将这三个数的最小值称为数列
,将这三个数的最小值称为数列![]() ,
,![]() ,
,![]() 的最佳值.例如,对于数列2,
的最佳值.例如,对于数列2,![]() ,3,因为
,3,因为![]() ,
,![]() ,
,![]() ,所以数列2,
,所以数列2,![]() ,3的最佳值为
,3的最佳值为![]() .
.
小明进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列![]() ,2,3的最佳值为
,2,3的最佳值为![]() ;数列3,
;数列3,![]() ,2的最佳值为1;
,2的最佳值为1;![]() .经过研究,小明发现,对于“2,
.经过研究,小明发现,对于“2,![]() ,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)求数列![]() ,
,![]() ,2的最佳值;
,2的最佳值;
(2)将“![]() ,
,![]() ,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将3,![]() ,
,![]() 这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求
这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com