
科目: 来源: 题型:
【题目】已知一次函数的图象经过点(3,2)和(1,4).
(1)画出此函数的图象;
(2)求此一次函数的表达式;
(3)若此函数的图象与x轴交于点A,与y轴交于点B,求线段AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由

查看答案和解析>>
科目: 来源: 题型:
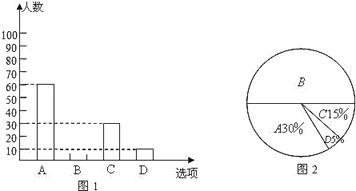
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A.1.5小时以上;B.1~1.5小时;C.0.5~1小时;D.0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在1小时以下.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,△AB'C和△ABC关于AC所在的直线对称,AD和B'C相交于点O,连接BB'
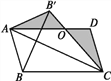
(1)请直接写出图中所有的等腰三角形(不添加字母);
(2)求证:△AB'O≌△CDO
查看答案和解析>>
科目: 来源: 题型:
【题目】将连续的正偶数2,4,6,8…,排成下表:
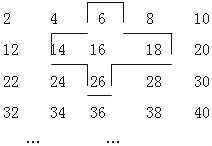
(1)十字框中的五个数的和是中间的数16的几倍?
(2)若将十字框上下左右移动,可框住另外的五个数,设中间的数为![]() ,用代数式表示十字框中的五个数的和;
,用代数式表示十字框中的五个数的和;
(3)这五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题探究
将几何图形按照某种法则或规则变换成另一种几何图形的过程叫做几何变换.旋转变换是几何变换的一种基本模型.经过旋转,往往能使图形的几何性质明白显现.题设和结论中的元素由分散变为集中,相互之间的关系清楚明了,从而将求解问题灵活转化.
问题提出:如图1,![]() 是边长为1的等边三角形,
是边长为1的等边三角形,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() ,求
,求![]() 的最小值.
的最小值.
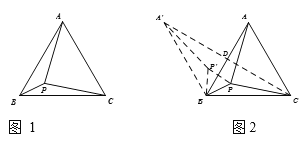
方法通过转化,把由三角形内一点发出的三条线段(星型线)转化为两定点之间的折线(化星为折),再利用“两点之间线段最短”求最小值(化折为直).
问题解决:如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() 、
、![]() ,记
,记![]() 与
与![]() 交于点
交于点![]() ,易知
,易知![]() ,
,![]() .由
.由![]() ,
,![]() ,可知
,可知![]() 为正三角形,有
为正三角形,有![]() .
.
故![]() .因此,当
.因此,当![]() 共线时,
共线时,![]() 有最小值是
有最小值是![]() .
.
学以致用:(1)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() 、
、![]() ,则
,则![]() 的最小值是__________.
的最小值是__________.
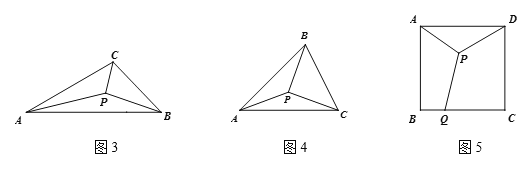
(2)如图4,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
(3)如图5,![]() 是边长为2的正方形
是边长为2的正方形![]() 内一点,
内一点,![]() 为边
为边![]() 上一点,连接
上一点,连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A,C都在直线l上,AE⊥AB且AE=AB,BC⊥CD且BC=CD,三点E,B,D到直线l的距离分别是6,3,4,计算图中由线段AB,BC,CD,DE,EA所围成的图形的面积是( )
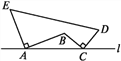
A. 50 B. 62 C. 65 D. 68
查看答案和解析>>
科目: 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.
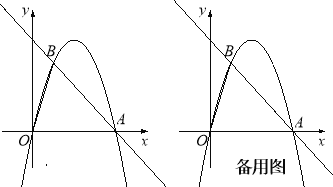
(1)求a,b的值;
(2)点P是线段AB上一动点(点P不与点A、B重合),过点P作PM∥OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,当S△ACN=S△PMN时,连接ON,点Q在线段BP上,过点Q作QR∥MN交ON于点R,连接MQ、BR,当∠MQR﹣∠BRN=45°时,求点R的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应环保组织提出的“低碳生活”的号召,李明决定不开汽车而改骑自行车上班.有一天,李明骑自行车从家里到工厂上班,途中因自行车发生故障,修车耽误了一段时间,车修好后继续骑行,直至到达工厂(假设在骑自行车过程中匀速行驶).李明离家的距离![]() (米)与离家时间
(米)与离家时间![]() (分钟)的关系表示如下图:
(分钟)的关系表示如下图:
(1)李明从家出发到出现故障时的速度为 米/分钟;
(2)李明修车用时 分钟;
(3)求线段BC所对应的函数关系式(不要求写出自变量的取值范围).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com