
科目: 来源: 题型:
【题目】已知抛物线c:y=x2+2x﹣3,将抛物线c平移得到抛物线c′,如果两条抛物线,关于直线x=1对称,那么下列说法正确的是( )
A. 将抛物线c沿x轴向右平移![]() 个单位得到抛物线c′ B. 将抛物线c沿x轴向右平移4个单位得到抛物线c′
个单位得到抛物线c′ B. 将抛物线c沿x轴向右平移4个单位得到抛物线c′
C. 将抛物线c沿x轴向右平移![]() 个单位得到抛物线c′ D. 将抛物线c沿x轴向右平移6个单位得到抛物线c′
个单位得到抛物线c′ D. 将抛物线c沿x轴向右平移6个单位得到抛物线c′
查看答案和解析>>
科目: 来源: 题型:
【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了的统计表和如图所示统计图.
组别 | 视力 | 频数(人) |
A |
| 20 |
B |
| a |
C |
| b |
D |
| 70 |
E |
| 10 |
请根据图表信息回答下列问题:
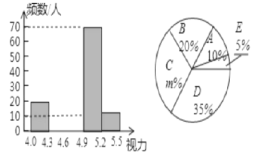
(1)求抽样调查的人数;
(2)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?根据上述信息估计该市今年八年级的学生视力正常的学生大约有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】借助一副三角板,可以得到一些平面图形
(1)如图1,∠AOC= 度.由射线OA,OB,OC组成的所有小于平角的和是多少度?
(2)如图2,∠1的度数比∠2度数的3倍还多30°,求∠2的度数;
(3)利用图3,反向延长射线OA到M,OE平分∠BOM,OF平分∠COM,请按题意补全图(3),并求出∠EOF的度数.
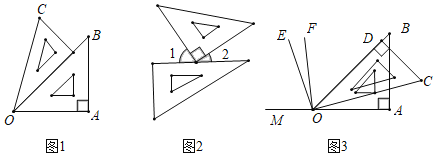
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB:y=![]() x+2与x轴、y轴分别交于A,B两点,C是第一象限内直线AB上一点,过点C作CD⊥x轴于点D,且CD的长为
x+2与x轴、y轴分别交于A,B两点,C是第一象限内直线AB上一点,过点C作CD⊥x轴于点D,且CD的长为![]() ,P是x轴上的动点,N是直线AB上的动点.
,P是x轴上的动点,N是直线AB上的动点.
(1)直接写出A,B两点的坐标;
(2)如图①,若点M的坐标为(0,![]() ),是否存在这样的P点.使以O,P,M,N为顶点的四边形是平行四边形?若有在,请求出P点坐标;若不存在,请说明理由.
),是否存在这样的P点.使以O,P,M,N为顶点的四边形是平行四边形?若有在,请求出P点坐标;若不存在,请说明理由.
(3)如图②,将直线AB绕点C逆时针旋转交y轴于点F,交x轴于点E,若旋转角即∠ACE=45°,求△BFC的面积.
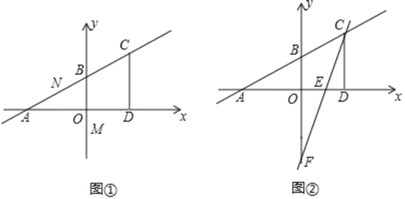
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某单位计划在室内安装空气净化装置,需购进A,B两种设备,每台B种设备价格比每台A种设备价格多700元,花3000元购买A种设备和花7200元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少元?
(2)根据单位实际情况,需购进A,B两种设备共20台,总费用不高于17000元,求A种设备至少要购买多少台?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
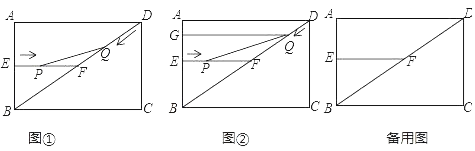
查看答案和解析>>
科目: 来源: 题型:
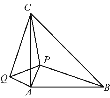
【题目】如图,在等腰△ABC中,∠CAB=90°,P是△ABC内一点,PA=1,PB=3,PC=![]() ,将△APB绕点A逆时针旋转后与△AQC重合.求:
,将△APB绕点A逆时针旋转后与△AQC重合.求:
(1)线段PQ的长;
(2)∠APC的度数.
查看答案和解析>>
科目: 来源: 题型:
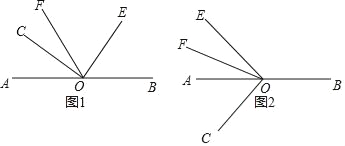
【题目】已知点O是AB上的一点,∠COE=90°,OF平分∠AOE.
(1)如图1,当点C,E,F在直线AB的同一侧时,若∠AOC=40°,求∠BOE和∠COF的度数;
(2)在(1)的条件下,∠BOE和∠COF有什么数量关系?请直接写出结论,不必说明理由;
(3)如图2,当点C,E,F分别在直线AB的两侧时,若∠AOC=β,那么(2)中∠BOE和∠COF的数量关系是否仍然成立?请写出结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com