
科目: 来源: 题型:
【题目】在平面直角坐标系中,△ABC 的位置如图所示:(每个小方格都是边长为 1 个单位长度的正方形)
(1)将△ABC 沿 y 轴方向向下平移 4 个单位长度得到![]() 则点
则点 ![]() 坐标为_______;
坐标为_______;
(2)将△ABC 绕着点 O 逆时针旋转 90°,画出旋转后得到的![]() ;
;
(3)直接写出点![]() ,
,![]() 的坐标.
的坐标.

查看答案和解析>>
科目: 来源: 题型:
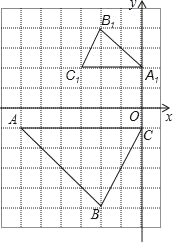
【题目】如图,△ABC与△A1B1C1是位似图形.
(1)在网格上建立平面直角坐标系,使得点A的坐标为(﹣6,﹣1),点C1的坐标为(﹣3,2),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,平面直角坐标系中,矩形OABC的顶点A(6,0)、B(6,4),D是BC的中点.动点P从O点出发,以每秒1个单位的速度,沿着OA、AB、BD运动.设P点运动的时间为t秒(0<t<13).

(1)写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(2)当点P在OA上运动时,连结CP.问:是否存在某一时刻t,当CP绕点P旋转时,点C能恰好落到AB的中点M处?若存在,请求出t的值并判断此时△CPM的形状;若不存在,请说明理由;
(3)当点P在AB上运动时,试探索当PO+PD的长最短时的直线PD的表达式。
查看答案和解析>>
科目: 来源: 题型:
【题目】某船从A码头顺流航行到B码头,然后逆流返行到C码头,共行9小时,已知船在静水中的速度为7.5千米/时,水流的速度为2.5千米/时,若A与C的距离为15千米,求A与B的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
查看答案和解析>>
科目: 来源: 题型:
【题目】在下边的日历中,用一个正方形任意圈出二行二列四个数,
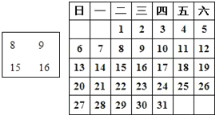
如

若在第一行第一列的那个数表示为![]() ,其余各数分别为
,其余各数分别为![]() ,
,![]() ,
,![]() .
.
(1)分别用含![]() 的代数式表示
的代数式表示![]() ,
,![]() ,
,![]() 这三个数;
这三个数;![]() = .
= .![]() = ,
= ,![]() = .
= .
(2)求这四个数的和(用含![]() 的代数式表示,要求合并同类项化简);
的代数式表示,要求合并同类项化简);
(3)这四个数的和会等于48吗?如果会,请算出此时![]() 的值,如果不会,说明理由.(要求列方程解答)
的值,如果不会,说明理由.(要求列方程解答)
(4)这四个数的和会等于112吗?如果会,请算出此时![]() 的值,如果不会,说明理由.(要求列方程解答)
的值,如果不会,说明理由.(要求列方程解答)
查看答案和解析>>
科目: 来源: 题型:
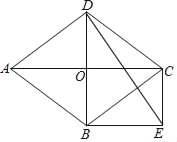
【题目】如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.
(1)求证:四边形OBEC是矩形;
(2)当∠ABD=60°,AD=2![]() 时,求∠EDB的正切值.
时,求∠EDB的正切值.
查看答案和解析>>
科目: 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
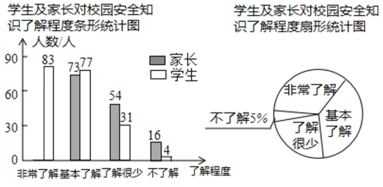
![]() 参与调查的学生及家长共有 人;
参与调查的学生及家长共有 人;
![]() 在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
![]() 在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
查看答案和解析>>
科目: 来源: 题型:
【题目】“奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是_____m.
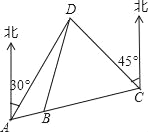
查看答案和解析>>
科目: 来源: 题型:
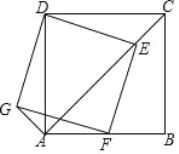
【题目】如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩 形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,求ME的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com