
科目: 来源: 题型:
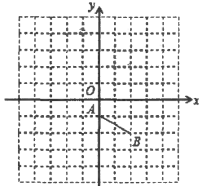
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系![]() 的原点
的原点![]() 在格点上,
在格点上,![]() 轴、
轴、![]() 轴都在格线上.线段
轴都在格线上.线段![]() 的两个端点也在格点上.
的两个端点也在格点上.
(1)若将线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,试在图中画出线段
,试在图中画出线段![]() .
.
(2)若线段![]() 与线段
与线段![]() 关于
关于![]() 轴对称,请画出线段
轴对称,请画出线段![]() .
.
(3)若点![]() 是此平面直角坐标系内的一点,当点
是此平面直角坐标系内的一点,当点![]() 四边围成的四边形为平行四边形 时,请你直接写出点
四边围成的四边形为平行四边形 时,请你直接写出点![]() 的坐标(写出一个即可).
的坐标(写出一个即可).
查看答案和解析>>
科目: 来源: 题型:
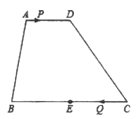
【题目】如图,在四边形![]() 中,
中,![]() ,
, ![]() 是
是![]() 的中点.点
的中点.点![]() 以每秒1个单位长度的速度从点
以每秒1个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以每秒3个单位长度的速度从 点
同时以每秒3个单位长度的速度从 点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.点
运动.点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.当运动时间
也随之停止运动.当运动时间![]() 秒时,以点
秒时,以点![]() 为顶点的四边形是平行四边形.则
为顶点的四边形是平行四边形.则![]() 的值为_________.
的值为_________.
查看答案和解析>>
科目: 来源: 题型:
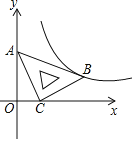
【题目】在平面直角坐标系![]() 中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标(1,0),顶点A的坐标为(0, 2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点
中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标(1,0),顶点A的坐标为(0, 2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点![]() 的坐标为__________
的坐标为__________
查看答案和解析>>
科目: 来源: 题型:
【题目】已知矩形0ABC在平面直角坐标系内的位置如图所示,点0为坐标原点,点A的坐标为(10,0),点B的坐标为(10,8),点Q为线段AC上-点,其坐标为(5,n).
(1)求直线AC的表达式
(2)如图,若点P为坐标轴上-动点,动点P沿折线AO→0C的路径以每秒1个单位长度的速度运动,到达C处停止求Δ0PQ的面积S与点P的运动时间t(秒)的函数关系式.
(3)若点P为坐标平面内任意-.点,是否存在这样的点P,使以0,C,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
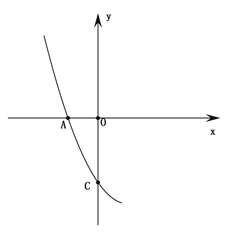
【题目】如图是二次函数y=ax2+bx+c(a≠0)的部分图像,其中点A(-1,0)是x轴上的一个交点,点C是y轴上的交点.
(1)若过点A的直线l与这个二次函数的图像的另一个交点为D,与该图像的对称轴交于点E,与y轴交于点F,且DE=EF=FA.
①求![]() 的值;
的值;
②设这个二次函数图像的顶点为P,问:以DF为直径的圆能否经过点P?若能,请求出此时二次函数的关系式;若不能,请说明理由.
(2)若点C坐标为(0,-1),设S=a+b+c ,求S的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知BC∥DE,BF平分∠ABC,DC平分∠ADE,则下列结论:①∠ACB=∠E;②DF平分∠ADC;③∠BFD=∠BDF;④∠ABF=∠BCD,其中正确的有( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目: 来源: 题型:
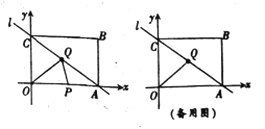
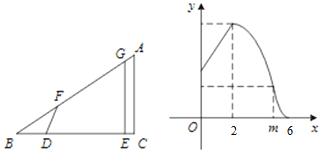
【题目】如图 , ![]() 中,
中, ![]() ,线段
,线段![]() 在射线
在射线![]() 上,且
上,且![]() ,线段
,线段![]() 沿射线
沿射线![]() 运动,开始时,点
运动,开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动停止,过点
时运动停止,过点![]() 作
作![]() ,与射线
,与射线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 相交于点
相交于点![]() .设
.设![]() ,四边形
,四边形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 关于
关于![]() 的函数图象如图所示(其中
的函数图象如图所示(其中![]() 时,函数的解析式不同)
时,函数的解析式不同)
(1)填空: ![]() 的长是 ;
的长是 ;
(2)求![]() 关于
关于![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个长方体纸盒的平面展开图如图所示,纸盒中相对两个面上的数互为相反数.
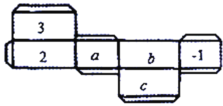
(1)填空:![]() ________,
________,![]() ________,
________,![]() ________.
________.
(2)先化简,再求值:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2017年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车?
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知A型车的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆.根据销售经验,A型车不少于B型车的2倍,但不超过B型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com