
科目: 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
科目: 来源: 题型:
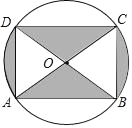
【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD,若AC=10cm,∠BAC=36°,则图中阴影部分的面积为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】数学活动课上,王老师说:“![]() 是无理数,无理数就是无限不循环小数,同学们,你能把
是无理数,无理数就是无限不循环小数,同学们,你能把![]() 的小数部分全部写出来吗?”大家议论纷纷,小明同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用
的小数部分全部写出来吗?”大家议论纷纷,小明同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用![]() ﹣1表示它的小数部分.”王老师说:“小明同学的说法是正确的,因为
﹣1表示它的小数部分.”王老师说:“小明同学的说法是正确的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分,”请你解答:
的整数部分是1,将这个数减去其整数部分,差就是小数部分,”请你解答:
(1)填空题:![]() 的整数部分是 ;小数部分是
的整数部分是 ;小数部分是
(2)已知8+![]() =x+y,其中x是一个整数,且0<y<1,求出2x+(y-
=x+y,其中x是一个整数,且0<y<1,求出2x+(y-![]() )2012的值.
)2012的值.
查看答案和解析>>
科目: 来源: 题型:
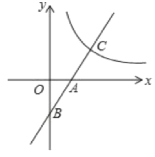
【题目】如图,已知一次函数y=2x2的图象与x,y轴分别交于点A,B,与反比例函数y=![]() (x>0)的图象交于点C,且AB=AC,则k的值为()
(x>0)的图象交于点C,且AB=AC,则k的值为()
A.5B.4C.3D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为美化校园,计划对面积为2000m2的区域进行绿化,安排甲、乙两个工程队完成,已知甲队每天完成绿化的面积是乙队每天完成绿化的面积的2倍,并且在独立完成面积为600m2区域的绿化时,甲队比乙队少用6天.
(1)甲、乙两个工程队每天能完成绿化的面积分别是多少?
(2)若学校每天需付给甲队的绿化费用为0.5万元,乙队为0.3万元,要使这次的绿化总费用不超过10万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目: 来源: 题型:
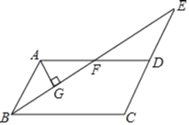
【题目】如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点.
(1)求证:△ABF≌△DEF;
(2)若AG⊥BE于G,BC=4,AG=1,求BE的长.
查看答案和解析>>
科目: 来源: 题型:
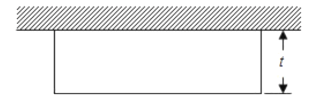
【题目】有长为l的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为t.
(1)用关于l,t的代数式表示园子的面积;这个代数式是多项式还是单项式?
(2)若l=100固定不变,若t的值取20,25,30时,则哪一种取法所围成的园子面积最大?
查看答案和解析>>
科目: 来源: 题型:
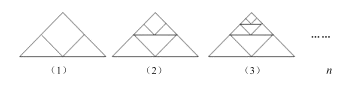
【题目】如下图所示,它们是一个按一定规律构造的,第(1)个图中有3个三角形,第(2)个图中有7个三角形,第(3)个图中有_____个三角形,依次规律第![]() 个图形中有__________个三角形.
个图形中有__________个三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=x2﹣2x+a(a<0)与y轴相交于点A,顶点为M.直线y=![]() x﹣a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x﹣a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
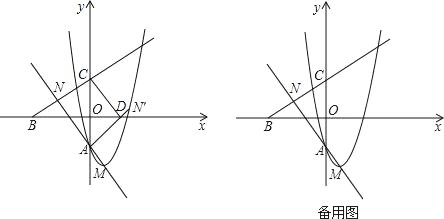
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x2﹣2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某快车的计费规则如表1,小明几次乘坐快车的情况如表2,请仔细观察分析表格解答以下问题:
(1)填空:a= ,b= ;
(2)列方程求解表1中的x;
(3)小明的爸爸23:10打快车从机场回家,快车行驶的平均速度是100公里/小时,到家后小明爸爸支付车费603元,请问机场到小明家的路程是多少公里?(用方程解决此问题)
表1:某快车的计费规则
里程费(元/公里) | 时长费(元/分钟) | 远途费(元/公里) | |||
5:00﹣23:00 | a | 9:00﹣18:00 | x | 12公里及以下 | 0 |
23:00﹣次日5:00 | 3.2 | 18:00﹣次日9:00 | 0.5 | 超出12公里的部分 | 1.6 |
(说明:总费用=里程费+时长费+远途费)
表2:小明几次乘坐快车信息
上车时间 | 里程(公里) | 时长(分钟) | 远途费(元) | 总费用(元) |
7:30 | 5 | 5 | 0 | 13.5 |
10:05 | 20 | 18 | 66.7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com