
科目: 来源: 题型:
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区. 已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市. 已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从C市运往B市的救灾物资为x吨.
(1)请填写下表;

(2)设C、D两市的总运费为W元,求W与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从C市到B市的路况得到了改善,缩短了运输时间,运费每吨减少n元(n>0),其余路线运费不变,若C、D两市的总运费的最小值不小于10080元,求n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A、B分别是x轴上位于原点左右两侧的点,点P在第一象限,且它的纵坐标为3,直线AP交y轴于点C(0,2),直线PB交y轴于点D,且ΔAOP的面积为6.

(1)求直线AP的关系式;
(2)若ΔBOP与ΔAOP的面积相等,求ΔBOD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
查看答案和解析>>
科目: 来源: 题型:
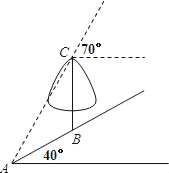
【题目】如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)
(参考数据:sin20°=0.34,tan20°=0.36,sin30°=0.50,tan30°=0.58,sin40°=0.64,tan40°=0.84,sin70°=0.94,tan70°=2.75)
查看答案和解析>>
科目: 来源: 题型:
【题目】为方便市民出行,减轻城市中心交通压力,贵阳市地铁1号线于2018年12月1号正式全线开通.地铁开通后,李明爸爸妈妈的出行方式将由乘公交车改为乘坐地铁,爸爸从国际生态会议中心站出发至喷水池站,每天所需的时间将比以往节省70%;妈妈从国际生态会议中心站出发至珠江路站,每天所需的时间将比以往节省55%,这样两人所需的时间共节省60%,现在两人乘地铁所需的时间之和为1.2小时.请问李明爸爸妈妈原来乘公交车上班时每天所需时间各为多少小时?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=x2﹣2x+c(c<0)的图象与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,且OB=OC.
(Ⅰ)求该抛物线的解析式和顶点坐标;
(Ⅱ)直线l是抛物线的对称轴,E是抛物线的顶点,连接BE,线段OC上的点F关于直线l的对称点F′恰好在线段BE上,求点F的坐标;
(Ⅲ)若有动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N,试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
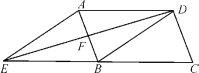
【题目】如图,在平行四边形ABCD中,DB=DA,∠ADB的平分线交AB于点F,交CB的延长线于点E,连接AE.
(1)求证:四边形AEBD是菱形;
(2)若DC=![]() ,EF:BF=3,求菱形AEBD的面积.
,EF:BF=3,求菱形AEBD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】为创建足球特色学校,营造足球文化氛围,某学校随机抽取部分八年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分—10分,B级:7分—7.9分,C级:6分—6.9分,D级:1分—5.9分)根据所给信息,解答以下问题:
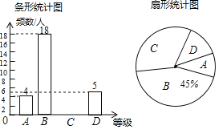
(1)样本容量为 ,C对应的扇形的圆心角是____度,补全条形统计图;
(2)所抽取学生的足球运球测试成绩的中位数会落在____等级;
(3)该校八年级有300名学生,请估计足球运球测试成绩达到![]() 级的学生有多少人?
级的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
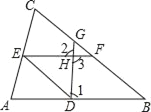
【题目】完成下面的证明过程
如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
证明:∵∠1+∠2=180°(已知),
而∠2=∠3(________),
∴∠1+∠3=180°
∴______∥______(________)
∴∠B=______(________)
∵∠B=∠DEF(已知)
∴∠DEF=______(等量代换)
∴DE∥BC(________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com