
科目: 来源: 题型:
【题目】为迎接4月23日的世界读书日,某书店制定了活动计划,如表是活动计划的部分信息:
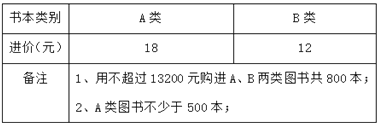
(1)杨经理查看计划时发现:A类图书的标价是B类图书标价的1.5倍.若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本.请求出A、B两类图书的标价.
(2)经市场调查后,杨经理发现他们高估了“读书日”对图书销售的影响,便调整了销售方案:A类图书每本按标价降低a元(![]() )销售,B类图书价格不变.那么书店应如何进货才能获得最大利润.
)销售,B类图书价格不变.那么书店应如何进货才能获得最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】世界卫生组织预计:到2025年,全世界将会有一半人面临用水危机,为了倡导“节约用水,从我做起”,某县政府决定对县直属机关300户家庭一年的月平均用水量进行调查,调查小组抽查了部分家庭月平均用水量(单位:吨),绘制条形图和扇形图如图所示.
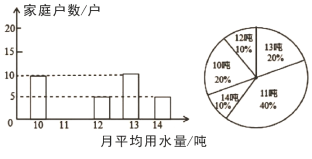
(1)请将条形统计图补充完整;
(2)这些家庭月平均用水量数据的平均数是_______,众数是______,中位数是_______;
(3)根据样本数据,估计该县直属机关300户家庭的月平均用水量不超过12吨的约有多少户.
查看答案和解析>>
科目: 来源: 题型:
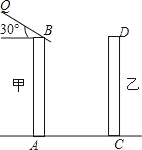
【题目】如图,是住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m,![]() =1.73);
=1.73);
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
查看答案和解析>>
科目: 来源: 题型:
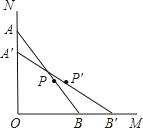
【题目】如图,一根木棒(AB)长为2a,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿N0向下滑动到A′,AA′=(![]() )a,B端沿直线OM向右滑动到B′,则木棒中点从P随之运动到P′所经过的路径长为_____.
)a,B端沿直线OM向右滑动到B′,则木棒中点从P随之运动到P′所经过的路径长为_____.
查看答案和解析>>
科目: 来源: 题型:
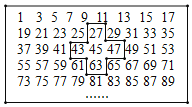
【题目】如图,将连续的奇数1,3,5,7……排成如下的数表,用十字形框框出5个数.
探究规律一:设十字框中间的奇数为x,则框中五个奇数的和用含x的整式表示为 ,这说明被十字框框中的五个奇数的和一定是正整数n(n>1)的倍数,这个正整数n是 ;
探究规律二:落在十字框中间且位于第二列的一组奇数是21,39,57,75,…,则这一组数可以用整式表示为18m+3(m为序数),同样,落在十字框中间且位于第三列的一组奇数可以表示为 ;(用含m的式子表示)
运用规律:
(1)已知被十字框框中的五个奇数的和为2025,则十字框中间的奇数是 ,这个奇数落在从左往右第 列;
(2)被十字框框中的五个奇数的和可能是2020吗?若能,请求出这五个数:若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
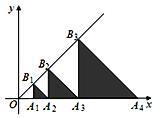
【题目】如图,△A1B1A2,△A2B2A3,△A3B3A4,...,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An,在x轴上,点B1、B2、…Bn在直线y=x上,已知OA1=1,则OA2019的长是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A=x-2y,B=-x-4y+1.
(1)求2(A+B)-(A-B);(结果用含x,y的代数式表示)
(2)当![]() 与
与![]() 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成![]() 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究![]() 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当![]() 时,
时,![]()
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当![]() 时,
时,![]()
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
综上所述,可得表①
| 3 | 4] | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三
角形?(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用![]() 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com